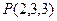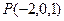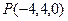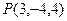题目内容
已知空间直角坐标系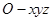 中有一点
中有一点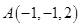 ,点
,点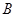 是
是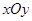 平面内的直线
平面内的直线 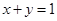 上的动点,则
上的动点,则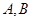 两点的最短距离是( )
两点的最短距离是( )
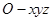 中有一点
中有一点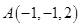 ,点
,点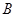 是
是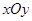 平面内的直线
平面内的直线 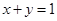 上的动点,则
上的动点,则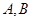 两点的最短距离是( )
两点的最短距离是( )A.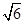 | B.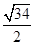 | C.3 | D.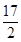 |
B
解:点B是xOy平面内的直线x+y=1上的动点,结合空间直角坐标系O-xyz中有一点A(-1,-1,2),
得到B(a,b,0), AB =(a+1,b+1,-2),直线的方向向量为 μ =(1,-1,0),
AB的最短距离,就是 AB • μ =0时的AB 的距离.
所以a+1-b-1=0,即a-b=0,因为B在直线x+y=1,所以a="b=1" 2 ,
B="(1" 2 ,1
2 ,1  2 ,0),
2 ,0),
AB2=" (1" 2 +1)2+(1
2 +1)2+(1  2 +1)2+(2-0)2 =" 34"
2 +1)2+(2-0)2 =" 34"  4;
4;
故选B.
得到B(a,b,0), AB =(a+1,b+1,-2),直线的方向向量为 μ =(1,-1,0),
AB的最短距离,就是 AB • μ =0时的AB 的距离.
所以a+1-b-1=0,即a-b=0,因为B在直线x+y=1,所以a="b=1" 2 ,
B="(1"
 2 ,1
2 ,1  2 ,0),
2 ,0),AB2=" (1"
 2 +1)2+(1
2 +1)2+(1  2 +1)2+(2-0)2 =" 34"
2 +1)2+(2-0)2 =" 34"  4;
4;故选B.

练习册系列答案
相关题目
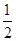 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).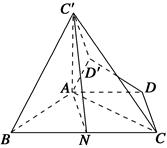
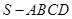 中,底面
中,底面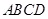 为平行四边形,侧面
为平行四边形,侧面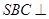 面
面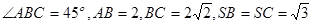
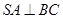 ;
;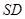 与面
与面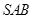 所成角的正弦值。
所成角的正弦值。
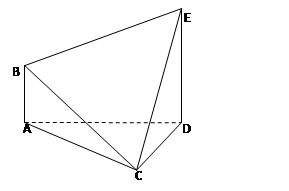
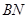 ⊥平面
⊥平面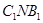 (2)求平面
(2)求平面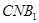 与平面
与平面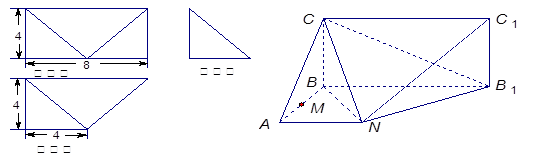
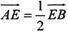 时,求二面角D1-EC-D的大小.
时,求二面角D1-EC-D的大小.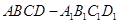 中,
中,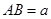 ,
,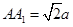 ,
,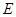 为
为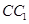 的中点,
的中点,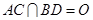 .
.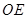 ∥平面
∥平面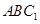 ;
;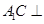 平面
平面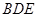 .
.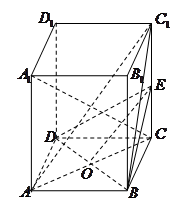
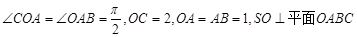 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.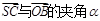 的余弦值;
的余弦值;
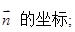
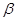 ,求
,求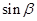 。
。
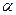 内有一点
内有一点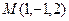 ,平面
,平面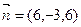 ,则下列点
,则下列点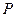 中,在平面
中,在平面