题目内容
如图,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB上一点
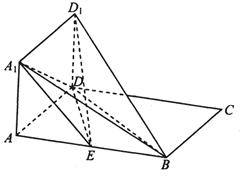
(I) 当点E为AB的中点时,求证;BD1//平面A1DE
(II)求点A1到平面BDD1的距离;
(III) 当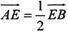 时,求二面角D1-EC-D的大小.
时,求二面角D1-EC-D的大小.

(I) 当点E为AB的中点时,求证;BD1//平面A1DE
(II)求点A1到平面BDD1的距离;
(III) 当
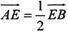 时,求二面角D1-EC-D的大小.
时,求二面角D1-EC-D的大小.(1)略 (2)A1到面BDD1的距离为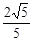 (3)D1-EC-D的大小为
(3)D1-EC-D的大小为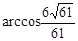
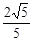 (3)D1-EC-D的大小为
(3)D1-EC-D的大小为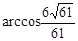
(I) 要证BD1//平面A1DE,只要证明BD1平行该面内的一条直线,取中点,由中位线可证得;(II)等积法求高;(III)可以用传统法找出平面角也可以向量法求。
解法一:(I)证明:连结AD1交A1D于F,则F为中点,连结EF,如图.

∵ E为中点,∴ EF//BD1.又EF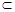 面A1DE,BD1
面A1DE,BD1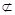 面A1DE,
面A1DE,
∴ BD1//面A1DE.……………3分
(II)在Rt△ABD中,AB=2AD=2,可得BD=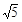 ,
,
∴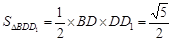 ,
,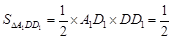 ,
,
设A1到面BDD1的距离为d,则由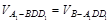 有
有
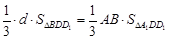 ,即
,即 ,解得
,解得 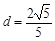 ,
,
即A1到面BDD1的距离为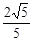 .……………………………………………8分
.……………………………………………8分
(III)连结EC.由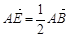 ,有
,有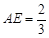 ,
,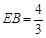 ,
,
过D作DH⊥EC于H,连结D1H,由已知面AA1D1D⊥面ABCD且DD1⊥AD,
∴DD1⊥面ABCD.由三垂线定理知:D1H⊥EC,∴ ∠DHD1为D1-EC-D的平面角.
Rt△EBC中,由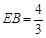 ,BC=1,得
,BC=1,得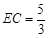 .又DH·EC=DC·BC,代入解得
.又DH·EC=DC·BC,代入解得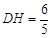 ,
,
∴在Rt△DHD1中,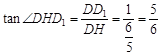 .∴
.∴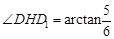 ,即二面角D1-EC-D的大小为
,即二面角D1-EC-D的大小为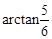 .…………12分
.…………12分
解法二:(I)同解法一.………………3分
(II)由面ABCD⊥面ADD1A,且四边形AA1D1D为正方形,四边形ABCD为矩形,可得D1D⊥AD,D1D⊥DC,DC⊥DA.
于是以D为原点,DA,DC,DD1分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.

由AB=2AD=2知:D(0,0,0),D1(0,0,1),A1(1,0,1),B(1,2,0),
∴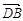 =(1,2,0),
=(1,2,0),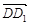 =(0,0,1),
=(0,0,1),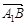 =(0,2,-1).设面BDD1的一个法向量为n1
=(0,2,-1).设面BDD1的一个法向量为n1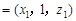 ,
,
则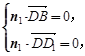 即
即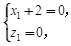 ∴
∴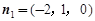 .
.
∴ 点A1到面BDD1的距离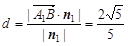 . …………………………8分
. …………………………8分
(III)由(II)及题意知:E(1,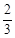 ,0),C(0,2,0),
,0),C(0,2,0),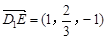 ,
,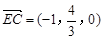 .
.
设面D1EC的一个法向量为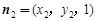 ,
,
则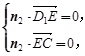 即
即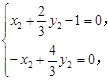 可得
可得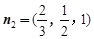 .
.
又易知面DEC的一个法向量是 (0,0,1),
(0,0,1),
设D1-EC-D的大小为θ,则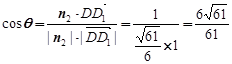 ,得
,得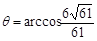 .
.
即D1-EC-D的大小为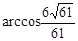
解法一:(I)证明:连结AD1交A1D于F,则F为中点,连结EF,如图.

∵ E为中点,∴ EF//BD1.又EF
 面A1DE,BD1
面A1DE,BD1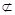 面A1DE,
面A1DE,∴ BD1//面A1DE.……………3分
(II)在Rt△ABD中,AB=2AD=2,可得BD=
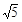 ,
,∴
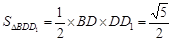 ,
,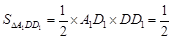 ,
,设A1到面BDD1的距离为d,则由
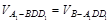 有
有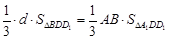 ,即
,即 ,解得
,解得 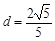 ,
,即A1到面BDD1的距离为
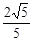 .……………………………………………8分
.……………………………………………8分(III)连结EC.由
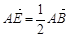 ,有
,有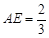 ,
,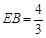 ,
,过D作DH⊥EC于H,连结D1H,由已知面AA1D1D⊥面ABCD且DD1⊥AD,
∴DD1⊥面ABCD.由三垂线定理知:D1H⊥EC,∴ ∠DHD1为D1-EC-D的平面角.
Rt△EBC中,由
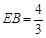 ,BC=1,得
,BC=1,得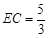 .又DH·EC=DC·BC,代入解得
.又DH·EC=DC·BC,代入解得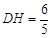 ,
,∴在Rt△DHD1中,
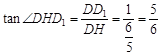 .∴
.∴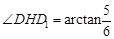 ,即二面角D1-EC-D的大小为
,即二面角D1-EC-D的大小为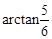 .…………12分
.…………12分解法二:(I)同解法一.………………3分
(II)由面ABCD⊥面ADD1A,且四边形AA1D1D为正方形,四边形ABCD为矩形,可得D1D⊥AD,D1D⊥DC,DC⊥DA.
于是以D为原点,DA,DC,DD1分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.

由AB=2AD=2知:D(0,0,0),D1(0,0,1),A1(1,0,1),B(1,2,0),
∴
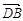 =(1,2,0),
=(1,2,0),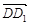 =(0,0,1),
=(0,0,1),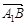 =(0,2,-1).设面BDD1的一个法向量为n1
=(0,2,-1).设面BDD1的一个法向量为n1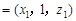 ,
,则
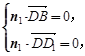 即
即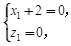 ∴
∴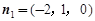 .
.∴ 点A1到面BDD1的距离
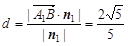 . …………………………8分
. …………………………8分(III)由(II)及题意知:E(1,
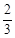 ,0),C(0,2,0),
,0),C(0,2,0),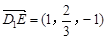 ,
,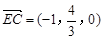 .
.设面D1EC的一个法向量为
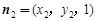 ,
,则
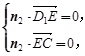 即
即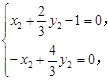 可得
可得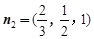 .
.又易知面DEC的一个法向量是
 (0,0,1),
(0,0,1),设D1-EC-D的大小为θ,则
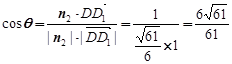 ,得
,得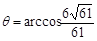 .
.即D1-EC-D的大小为
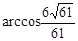

练习册系列答案
相关题目
 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.
 -
- 中,
中, 分别为
分别为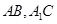 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 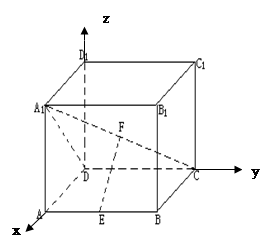
 平面
平面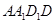 ;
;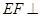 平面
平面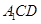 .
. ,使得平面
,使得平面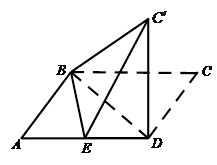
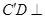 平面ABD;
平面ABD;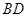 与平面
与平面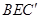 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.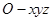 中有一点
中有一点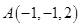 ,点
,点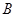 是
是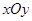 平面内的直线
平面内的直线 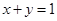 上的动点,则
上的动点,则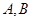 两点的最短距离是( )
两点的最短距离是( )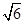
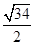
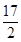
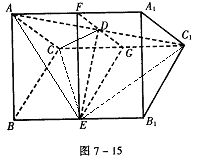
 中,
中,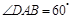 .点
.点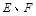 分别在边
分别在边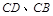 上,点
上,点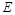 与点
与点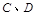 不重合,
不重合,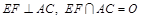 .沿
.沿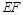 将
将 翻折到
翻折到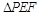 的位置,使平面
的位置,使平面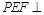 平面
平面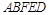 .
.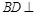 平面
平面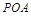 ;
;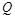 满足
满足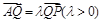 ,试探究:当
,试探究:当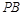 取得最小值时,直线
取得最小值时,直线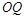 与平面
与平面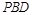 所成角的大小是否一定大于
所成角的大小是否一定大于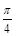 ?并说明理由.
?并说明理由.
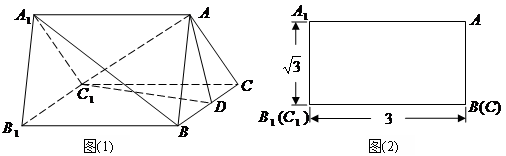
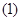 是一个水平放置的正三棱柱
是一个水平放置的正三棱柱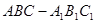 ,
,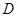 是棱
是棱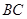 的中点.正三棱柱的主视图如图
的中点.正三棱柱的主视图如图 .
.
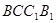 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明) .
.
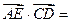 _ ▲ .
_ ▲ .