题目内容
在等腰梯形ABCD中,AD∥BC,AD=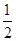 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
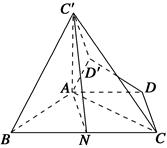
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
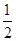 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
(1)见解析(2)见解析(3)-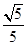
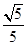
(1)证明 ∵AD=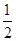 BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,
BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,
∴四边形ANCD是菱形,∴∠ACB=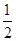 ∠DCB=30°,
∠DCB=30°,
∴∠BAC=90°,即AC⊥AB,又平面C′BA⊥平面ABC,平面C′BA∩平面ABC=AB,∴AC⊥平面ABC′.
(2)证明:∵AD∥BC,AD′∥BC′,AD∩AD′=A,BC∩BC′=B,∴平面ADD′∥平面BCC′,又C′N?平面BCC′,∴C′N∥平面ADD′.
(3)解:∵AC⊥平面ABC′,AC′⊥平面ABC.
如图建立空间直角坐标系,
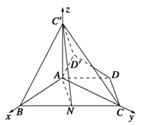
设AB=1,则B(1,0,0),C(0, ,0),C′(0,0,
,0),C′(0,0, ),
),
N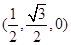 ,∴
,∴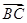 ′=(-1,0,
′=(-1,0, ),
),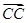 ′=(0,-
′=(0,- ,
, ),设平面C′NC的法向量为n=(x,y,z),则
),设平面C′NC的法向量为n=(x,y,z),则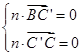 即
即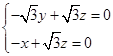
取z=1,则x= ,y=1,∴n=(
,y=1,∴n=( ,1,1).
,1,1).
∵AC′⊥平面ABC,∴平面C′AN⊥平面ABC,又BD⊥AN,平面C′AN∩平面ABC=AN,∴BD⊥平面C′AN,BD与AN交于点O,O则为AN的中点,O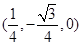 ,∴平面C′AN的法向量
,∴平面C′AN的法向量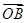 =
=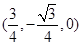 .
.
∴cos〈n,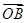 〉=
〉=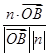 =
=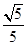 ,
,
由图形可知二面角AC′NC为钝角,
所以二面角AC′NC的余弦值为-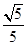
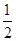 BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,
BC,N是BC的中点,∴AD=NC,又AD∥BC,∴四边形ANCD是平行四边形,∴AN=DC,又∠ABC=60°,∴AB=BN=AD,∴四边形ANCD是菱形,∴∠ACB=
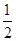 ∠DCB=30°,
∠DCB=30°,∴∠BAC=90°,即AC⊥AB,又平面C′BA⊥平面ABC,平面C′BA∩平面ABC=AB,∴AC⊥平面ABC′.
(2)证明:∵AD∥BC,AD′∥BC′,AD∩AD′=A,BC∩BC′=B,∴平面ADD′∥平面BCC′,又C′N?平面BCC′,∴C′N∥平面ADD′.
(3)解:∵AC⊥平面ABC′,AC′⊥平面ABC.
如图建立空间直角坐标系,

设AB=1,则B(1,0,0),C(0,
 ,0),C′(0,0,
,0),C′(0,0, ),
),N
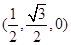 ,∴
,∴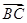 ′=(-1,0,
′=(-1,0, ),
),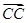 ′=(0,-
′=(0,- ,
, ),设平面C′NC的法向量为n=(x,y,z),则
),设平面C′NC的法向量为n=(x,y,z),则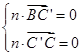 即
即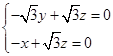
取z=1,则x=
 ,y=1,∴n=(
,y=1,∴n=( ,1,1).
,1,1).∵AC′⊥平面ABC,∴平面C′AN⊥平面ABC,又BD⊥AN,平面C′AN∩平面ABC=AN,∴BD⊥平面C′AN,BD与AN交于点O,O则为AN的中点,O
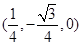 ,∴平面C′AN的法向量
,∴平面C′AN的法向量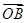 =
=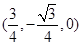 .
.∴cos〈n,
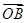 〉=
〉=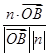 =
=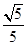 ,
,由图形可知二面角AC′NC为钝角,
所以二面角AC′NC的余弦值为-

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
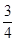 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4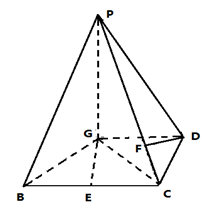
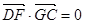 ,
,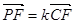 ,求
,求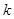 的值.
的值.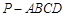 的底面
的底面 是直角梯形,
是直角梯形,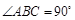 ,
,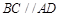 ,且
,且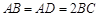 ,顶点
,顶点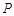 在底面
在底面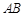 的中点
的中点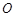 上.
上.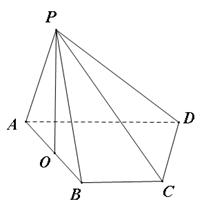
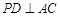 ;
;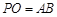 ,求直线
,求直线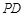 与
与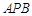 与平面
与平面 所成的二面角为
所成的二面角为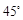 ,求
,求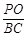 的值.
的值.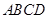 为直角梯形,
为直角梯形,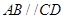 ,
,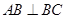 ,
,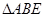 为等边三角形,且平面
为等边三角形,且平面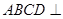 平面
平面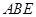 ,
,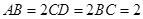 ,
,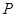 为
为 中点.
中点.
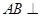
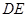 ;
;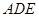 与平面
与平面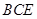 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;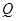 ,使
,使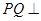 平面
平面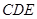 ,如果存在,求
,如果存在,求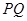 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. 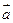 =(3,4),
=(3,4),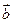 =(-2,y),且3
=(-2,y),且3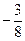
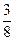
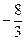
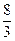
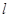 的法向量为
的法向量为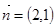 ,则该直线的倾斜角为 .(用反三角函数值表示)
,则该直线的倾斜角为 .(用反三角函数值表示)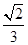 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.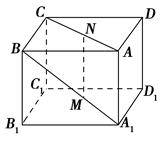
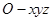 中有一点
中有一点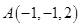 ,点
,点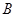 是
是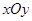 平面内的直线
平面内的直线 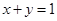 上的动点,则
上的动点,则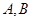 两点的最短距离是( )
两点的最短距离是( )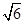
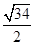
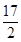
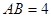
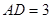
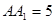 则 .
则 .