题目内容
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1。
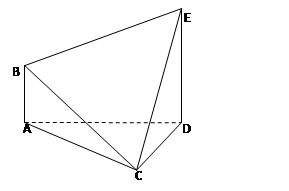
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
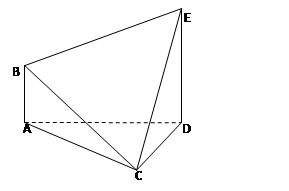
(1)请在线段CE上找到一点F,使得直线BF∥平面ACD,并证明;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(1)点F应是线段CE的中点(2)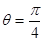
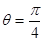
试题分析:解:以D点为原点建立如图所示的空间直角坐标系,使得
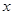 轴和
轴和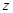 轴的正半轴分别经过点A和点E,则各点的坐标为
轴的正半轴分别经过点A和点E,则各点的坐标为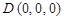 ,
,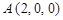 ,
,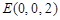 ,
,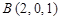 ,
,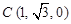 ,
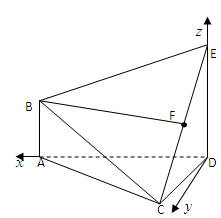
,
(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为
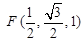 ,∴
,∴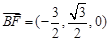
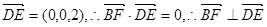 ,而
,而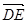 是平面ACD的一个法向量,此即证得BF∥平面ACD;
是平面ACD的一个法向量,此即证得BF∥平面ACD;(2)设平面BCE的法向量为
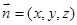 ,则
,则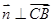 ,且
,且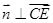 ,
,由
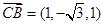 ,
,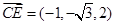 ,
,∴
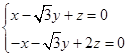 ,不妨设
,不妨设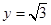 ,则
,则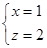 ,即
,即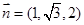 ,
,∴所求角
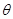 满足
满足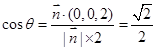 ,∴
,∴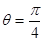 ;
;点评:在立体几何中,常考的知识点是:几何体的表面积与体积、直线与平面平行的判定定理、直线与平面垂直的判定定理和二面角。对于二面角,建立空间直角坐标系能使问题简化。

练习册系列答案
相关题目
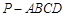 的底面
的底面 是直角梯形,
是直角梯形,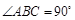 ,
,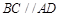 ,且
,且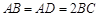 ,顶点
,顶点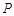 在底面
在底面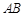 的中点
的中点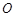 上.
上.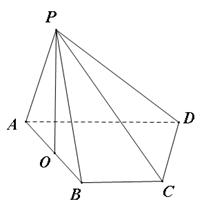
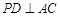 ;
;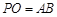 ,求直线
,求直线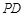 与
与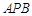 与平面
与平面 所成的二面角为
所成的二面角为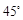 ,求
,求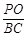 的值.
的值.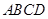 -
-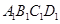 中,
中,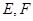 分别为
分别为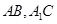 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 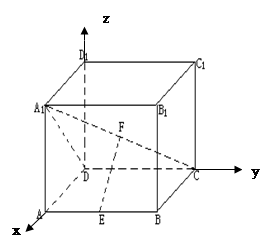
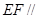 平面
平面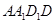 ;
;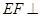 平面
平面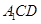 .
.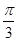 ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.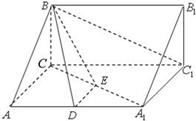
 ,使得平面
,使得平面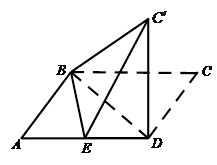
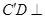 平面ABD;
平面ABD;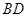 与平面
与平面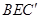 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.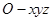 中有一点
中有一点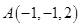 ,点
,点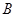 是
是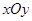 平面内的直线
平面内的直线 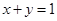 上的动点,则
上的动点,则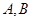 两点的最短距离是( )
两点的最短距离是( )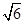
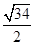
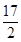
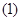 是一个水平放置的正三棱柱
是一个水平放置的正三棱柱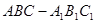 ,
,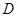 是棱
是棱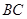 的中点.正三棱柱的主视图如图
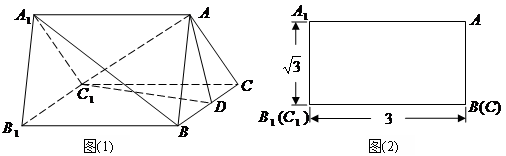
的中点.正三棱柱的主视图如图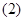 .
.
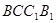 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)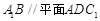 .
.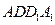 和三棱锥
和三棱锥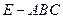 组合而成,点
组合而成,点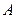 、
、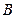 、
、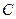 在圆
在圆 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中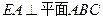 ,
,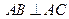 ,
,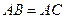 ,
,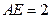 .
.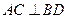 ;
;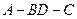 的平面角的大小.
的平面角的大小.
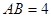
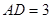
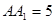 则 .
则 .