题目内容
16.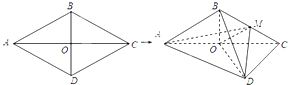 如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:
如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:(1)OM∥平面ABD;
(2)平面ABC⊥平面MDO.
分析 (1)证明OM∥AB.利用直线与平面平行的判定定理证明OM∥平面ABD.
(2)利用勾股定理证明OD⊥OM,证明OD⊥AC,然后证明OD⊥平面ABC,利用平面与平面垂直的判定定理证明平面ABC⊥平面MDO.
解答 证明:(1)由题意知,O为AC的中点,∵M为BC的中点,∴OM∥AB.,------------------------(2分).又∵OM?平面ABD,BC?平面ABD.
∴OM∥平面ABD,------------------------(6分)
(2)由题意可知:OM=OD=3,DM=$3\sqrt{2}$,∴OM2+OD2=DM2.
∴∠DOM=90°,即OD⊥OM,------------------------(8分)
又∵四边形ABCD是菱形,∴OD⊥AC,
∵OM∩AC=O,AC?平面ABC,
∴OD⊥平面ABC,------------------------(10分)
∵OD?平面ADO,
∴平面ABC⊥平面MDO,------------------------(12分)
点评 本题考查直线与平面平行,平面与平面垂直的判定定理的应用,考查空间想象能力逻辑推理能力.

练习册系列答案
相关题目
 一个类似杨辉三角形的数阵:则第九行的第二个数为66.
一个类似杨辉三角形的数阵:则第九行的第二个数为66.