题目内容
11.已知动点P到点F(1,0)的距离比到直线l:x+2=0距离小1.设动点P的轨迹为C,(Ⅰ)求轨迹C的方程;
(Ⅱ)已知定点M(4,0).斜率为k的直线交轨迹C于A、B两点,使△ABM成为以AB为底边的等腰三角形,
①求斜率k的取值范围;
②求弦长|AB|的最大值.
分析 (Ⅰ)根据条件结合抛物线的定义即可求轨迹C的方程;
(Ⅱ)设直线方程联立直线和抛物线方程转化为一元二次方程,利用等腰三角形的性质即可求出斜率以及弦长的最值.
解答 解:(Ⅰ)设P(x,y),由题意可得,P在直线x+2=0右边,
所以P点到直线x=-1和到F(1,0)距离相等,
所以P点的轨迹是顶点在原点,F为焦点,开口向右的抛物线,
∵F和顶点的距离=$\frac{p}{2}$=1,2p=4,所以轨迹C的方程是y2=4x.…(4分)
(Ⅱ) ①设直线AB的方程为y=kx+b,联立抛物线y2=4x,消元得:k2x2+(2kb-4)x+b2=0,
设A(x1,y1),B(x2,y2)及AB中点为N(x0,y0),
则${x_0}=\frac{{{x_1}+{x_2}}}{2}=\frac{2-kb}{k^2}$,y0=kx0+b=$\frac{2}{k}$…(6分)
∵AM=BM,∴MN⊥AB,∴kMN•kAB=-1,即$\frac{{\frac{2}{k}}}{{\frac{2-kb}{k^2}-4}}•k=\frac{2k}{{2-kb-4{k^2}}}•k$=-1,
得2-kb=2k2,$b=\frac{2}{k}-2k$,…(8分)
由△=16-16kb=$16(2{k^2}-1)>0⇒{k^2}>\frac{1}{2}$,∴$k>\frac{{\sqrt{2}}}{2}$或$k<-\frac{{\sqrt{2}}}{2}$,…(10分);
②$|{AB}|=\sqrt{1+{k^2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=4\sqrt{1+{k^2}}•\frac{{\sqrt{1-kb}}}{k^2}=4\sqrt{1+{k^2}}\frac{{\sqrt{2{k^2}-1}}}{k^2}$=$4\sqrt{\frac{{2{k^4}+{k^2}-1}}{k^4}}=4\sqrt{-\frac{1}{k^4}+\frac{1}{k^2}+2}$.…(12分)
令$\frac{1}{k^2}=t,则0<t<2$,∴$|AB|=4\sqrt{-{t^2}+t+2}=4\sqrt{-{{(t-\frac{1}{2})}^2}+\frac{9}{4}}≤6$.
所以弦长|ΑΒ|的最大为6.…(15分)
点评 本题主要考查曲线方程的求解,根据抛物线的定义建立方程关系是解决本题的关键.联系直线和抛物线方程,利用直线和抛物线相交的弦长公式求出弦长的最值,考查学生的运算能力.

| A. | 360 | B. | 180 | C. | 90 | D. | 45 |
| A. | $\sqrt{3}$-1 | B. | 2-$\sqrt{3}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
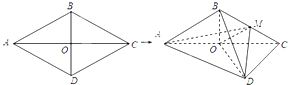 如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:
如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证: