题目内容
8.设△ABC的三内角A,B,C的对边分别为a,b,c,其面积为S,(1)若S=$\frac{1}{12\sqrt{3}}$(3a2+b2+6c2),用b,c表示sin(A+$\frac{π}{6}$),并求∠A的大小.
(2)当∠A取(1)中的值且△ABC为锐角三角形时,求cos2B-sin2C的取值范围.
分析 (1)把 S=$\frac{1}{2}$bc•sinA、余弦定理代入S=$\frac{1}{12\sqrt{3}}$(3a2+b2+6c2),利用基本不等式求得sin(A+$\frac{π}{6}$)=1,可得A的值.
(2)由条件求得-$\frac{π}{3}$<B-C<$\frac{π}{3}$,利用三角恒等变换化简cos2B-sin2C 为$\frac{1}{2}$cos$\frac{B-C}{2}$,求得 $\frac{1}{2}$cos$\frac{B-C}{2}$ 的范围,从而求得cos2B-sin2C的取值范围.
解答 解:(1)∵S=$\frac{1}{2}$bc•sinA,a2=b2+c2-2bc•cosA,代入S=$\frac{1}{12\sqrt{3}}$(3a2+b2+6c2),
可得 $\frac{1}{2}$bc•sinA=$\frac{1}{12\sqrt{3}}$(4b2-6bc•cosA+9c2),化简可得sin(A+$\frac{π}{6}$)=$\frac{{4a}^{2}{+9c}^{2}}{12bc}$≥$\frac{12bc}{12bc}$=1,
故有sin(A+$\frac{π}{6}$)=1,∴A+$\frac{π}{6}$=$\frac{π}{2}$,A=$\frac{π}{3}$.
(2)当∠A=$\frac{π}{3}$,且△ABC为锐角三角形时,则有-$\frac{π}{3}$<B-C<$\frac{π}{3}$,求cos2B-sin2C=$\frac{1+cos2B}{2}$-$\frac{1-cos2C}{2}$
=$\frac{cos2B+cos2C}{2}$=cos$\frac{B+C}{2}$cos$\frac{B-C}{2}$=$\frac{1}{2}$cos$\frac{B-C}{2}$,
∴$\frac{1}{4}$<$\frac{1}{2}$cos$\frac{B-C}{2}$≤$\frac{1}{2}$,即cos2B-sin2C的取值范围为($\frac{1}{4}$,$\frac{1}{2}$].
点评 本题主要考查余弦定理、基本不等式、三角恒等变换,余弦函数的定义域和值域,属于中档题.

| A. | 360 | B. | 180 | C. | 90 | D. | 45 |
| A. | $\sqrt{3}$-1 | B. | 2-$\sqrt{3}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{2-\sqrt{3}}{2}$ |
| A. | x2-8y2=1 | B. | 2x2-4y2=1 | C. | 8y2-x2=1 | D. | 4x2-2y2=1 |
 如图,在△ABC中,E、F分别为AC、AB的中点,BE与CF相交于G点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AG}$.
如图,在△ABC中,E、F分别为AC、AB的中点,BE与CF相交于G点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AG}$.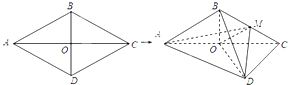 如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:
如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证: