题目内容
5. 一个类似杨辉三角形的数阵:则第九行的第二个数为66.
一个类似杨辉三角形的数阵:则第九行的第二个数为66.
分析 观察首尾两数都是1,3,5,7等为奇数,可知第n行的首尾两数,设第n(n≥2)行的第2个数构成数列{an},则有a3-a2=3,a4-a3=5,a5-a4=7,…,an-an-1=2n-3,相加得an,即可求出第九行的第二个数.
解答 解:观察首尾两数都是1,3,5,7,可知第n行的首尾两数均为2n-1
设第n(n≥2)行的第2个数构成数列{an},则有a3-a2=3,a4-a3=5,a5-a4=7,…,an-an-1=2n-3,
相加得an-a2=3+5+…+(2n-3)=$\frac{3+2n-3}{2}$×(n-2)=n(n-2)
an=3+n(n-2)=n2-2n+3,
所以第九行的第二个数为81-18+3=66.
故答案为:66.
点评 本题主要考查了数列的应用,以及利用叠加法求数列的通项,同时考查了等差数列求和,属于中档题.

练习册系列答案
相关题目
13.经过点(1,$\frac{1}{2}$),渐近线与圆(x-3)2+y2=1相切的双曲线的标准方程为( )
| A. | x2-8y2=1 | B. | 2x2-4y2=1 | C. | 8y2-x2=1 | D. | 4x2-2y2=1 |
10.三棱锥S-ABC的三视图如图,若点S,A,B,C都在球O的球面上,则球O的表面积是( )
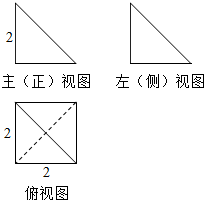

| A. | 4π | B. | 8π | C. | 12π | D. | 15π |
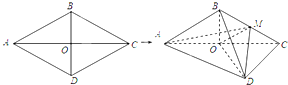 如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:
如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证: