题目内容
1.如图,在长方体ABCD-A1B1C1D1中,AB=2BC=2BB1,沿平面C1BD把这个长方体截成两个几何体:几何体(1);几何体(2)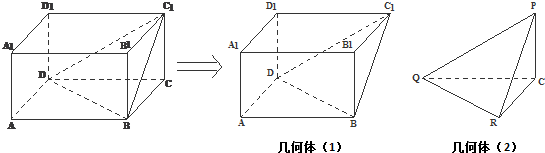
( I)设几何体(1)、几何体(2)的体积分为是V1、V2,求V1与V2的比值
( II)在几何体(2)中,求二面角P-QR-C的正切值.
分析 ( I)根据空间几何体的形状结合棱锥和棱柱的体积公式即可求几何体(1)、几何体(2)的体积以及求V1与V2的比值.
( II)求出二面角的平面角,结合三角形的边角关系即可求出二面角的大小.
解答 解( I)设BC=a,则AB=2a,BB1=a,所以${V_{ABCD-{A_1}{B_1}{C_1}{D_1}}}=2a×a×a=2{a^3}$---------(2分)
因为${V_2}=\frac{1}{3}{S_{△CQR}}×PC=\frac{1}{3}×\frac{1}{2}×2a×a×a=\frac{1}{3}{a^3}$--------------------------(4分)
${V_1}={V_{ABCD-{A_1}{B_1}{C_1}{D_1}}}-{V_2}=2{a^3}-\frac{1}{3}{a^3}=\frac{5}{3}{a^3}$----------------------(5分)
所以$\frac{V_1}{V_2}=\frac{{\frac{5}{3}{a^3}}}{{\frac{1}{3}{a^3}}}=5$------------(6分)
( II)由点C作CH⊥QR于点H,连结PH,因为PC⊥面CQR,QR?面CQR,所以PC⊥QR
因为PC∩CH=C,所以QR⊥面PCH,又因为PH?面PCH,
所以QR⊥PH,所以∠PHC是二面角P-QR-C的平面角--------------------(9分)
而$CH•QR=CQ•CR,CH×\sqrt{5}a=a×2a,CH=\frac{2a}{{\sqrt{5}}}$
所以$tan∠PHC=\frac{a}{{\frac{2a}{{\sqrt{5}}}}}=\frac{{\sqrt{5}}}{2}$------------------------------(12分)
点评 本题主要考查空间几何体的体积的计算以及空间二面角的求解,要求熟练掌握空间几何体的体积的计算公式以及二面角平面角的求解,考查学生的推理能力.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | (1,$\frac{4}{3}$) | B. | ($\frac{4}{3}$,$\sqrt{2}$) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |
| A. | x2-8y2=1 | B. | 2x2-4y2=1 | C. | 8y2-x2=1 | D. | 4x2-2y2=1 |

| A. | 4π | B. | 8π | C. | 12π | D. | 15π |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F(1,0),是椭圆C的右焦点,若不经过原点O的直线l:y=kx+m(k>0)与椭圆C相交于不同的两点A、B,记直线OA,OB的斜率分别为k1,k2,且k1•k2=k2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,F(1,0),是椭圆C的右焦点,若不经过原点O的直线l:y=kx+m(k>0)与椭圆C相交于不同的两点A、B,记直线OA,OB的斜率分别为k1,k2,且k1•k2=k2.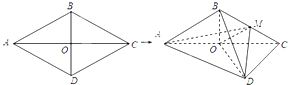 如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证:
如图,菱形ABCD的边长为6,∠BAD=60°,对角线AC,BD相交于点O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3$\sqrt{2}$.求证: 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.点E是线段BD的中点,点F是线段PD上的动点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD.点E是线段BD的中点,点F是线段PD上的动点.