题目内容
1．函数y=$\frac{（x+2）^{2}-4}{{x}^{2}+4x+4}$的单调区间是减区间（-∞，-2），增区间（-2，+∞）．分析 求y′，所以找使y′＞0，和使y′＜0的区间，从而找出原函数的单调区间．
解答 解：y′=$\frac{8（x+2）}{（{x}^{2}+4x+4）^{2}}$；
原函数的定义域为{x|x≠-2}；
∴x＞-2时，y′＞0；x＜-2时，y′＜0；
∴原函数的单调减区间是（-∞，-2），增区间是（-2，+∞）．
故答案为：减区间（-∞，-2），增区间（-2，+∞）．
点评 考查函数导数符号和函数单调性的关系，以及根据导数求函数单调区间的方法．
练习册系列答案
相关题目
6．已知双曲线Γ：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F，以原点为圆心，OF为半径的圆分别与双曲线Γ的一条渐近线及双曲线Γ交于M、N两点（其中M、N均为第一象限上的点），当MF∥ON时，双曲线Γ的离心离一定在区间（ ）
| A． | （1，$\frac{4}{3}$） | B． | （$\frac{4}{3}$，$\sqrt{2}$） | C． | （$\sqrt{2}$，$\sqrt{3}$） | D． | （$\sqrt{3}$，2） |
如图，在△ABC中，E、F分别为AC、AB的中点，BE与CF相交于G点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，试用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AG}$．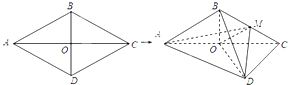
如图，菱形ABCD的边长为6，∠BAD=60°，对角线AC，BD相交于点O，将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=3$\sqrt{2}$．求证：