题目内容
6．求函数y=2sinx-3cosx的周期和最值．分析 利用两角和与差的正弦函数将解析式化为一个角的一个三角函数的形式，然后利用正弦函数的性质求周期和最值．
解答 解：y=2sinx-3cosx=$\sqrt{{2}^{2}+{3}^{2}}sin（x-θ）$=$\sqrt{13}$sin（x-θ）；其中tanθ=$\frac{3}{2}$．
所以y=2sinx-3cosx的周期为2π，最大值为$\sqrt{13}$，最小值为-$\sqrt{13}$．
点评 本题考查了对于y=asinx+bcosx的周期以及最值的求法；关键是利用两角和与差的正弦函数将解析式化为一个角的一个三角函数的形式，然后利用正弦函数的性质求周期和最值．
练习册系列答案
相关题目
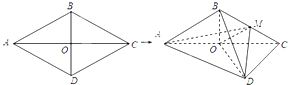如图，菱形ABCD的边长为6，∠BAD=60°，对角线AC，BD相交于点O，将菱形ABCD沿对角线AC折起，得到三棱锥B-ACD，点M是棱BC的中点，DM=3$\sqrt{2}$．求证：