题目内容
设函数f (x)="2cosx" (cosx+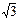 sinx)-1,x∈R
sinx)-1,x∈R
小题1:求f (x)的最小正周期T;
小题2:求f (x)的单调递增区间.
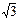 sinx)-1,x∈R
sinx)-1,x∈R小题1:求f (x)的最小正周期T;
小题2:求f (x)的单调递增区间.
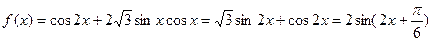 ………… 6分
………… 6分小题1:
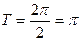 . ………… 9分
. ………… 9分小题2:由2kp –
 £ 2x +
£ 2x +  £ 2kp +
£ 2kp +  , 得:kp –
, 得:kp –  £ x £ kp +
£ x £ kp +  (k ÎZ),
(k ÎZ),f ( x ) 单调递增区间是[kp –
 ,kp +
,kp + ](k ÎZ) . ……………… 12
](k ÎZ) . ……………… 12同答案

练习册系列答案
相关题目
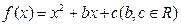 ,已知不论
,已知不论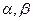 为何实数恒有
为何实数恒有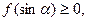
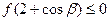 .
.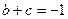 ;
;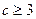 ;
;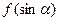 的最大值为8,求
的最大值为8,求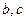 的值.
的值. (x≠a).
(x≠a). (x -
(x - )
) ,求m的集合M .
,求m的集合M .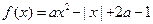
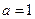 ,求
,求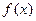 的单调区间;
的单调区间;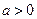 ,设
,设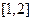 的最小值为
的最小值为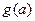 ,求
,求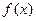 在
在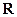 上是偶函数,在区间
上是偶函数,在区间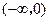 上递增,且有
上递增,且有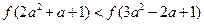 ,求
,求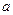 的取值范围.
的取值范围. 在
在
 上的最大值为3,最小值为2,求实数
上的最大值为3,最小值为2,求实数 的取值范围.
的取值范围.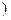 上单调递增,则b的取值范围是_________.
上单调递增,则b的取值范围是_________. 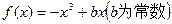 ,且
,且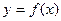 在区间(0,1)上单调递增,并且函数
在区间(0,1)上单调递增,并且函数