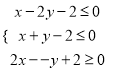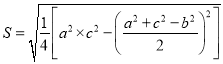题目内容
【题目】已知双曲线![]() =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0).
(1)若双曲线的一条渐近线方程为y=x且c=2,求双曲线的方程;
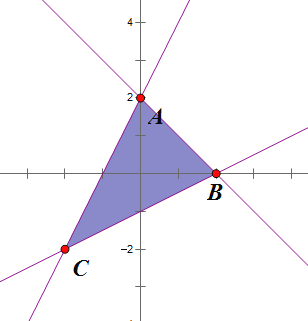
(2)以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过A作圆的切线,斜率为-![]() ,求双曲线的离心率.
,求双曲线的离心率.
【答案】(1)![]() =1(2)
=1(2)![]()
【解析】(1)∵双曲线的渐近线为y=±![]() x,∴a=b,
x,∴a=b,
∴c2=a2+b2=2a2=4,∴a2=b2=2,∴双曲线方程为![]() =1.
=1.
(2)设点A的坐标为(x0,y0),
∴直线AO的斜率满足![]() ·(-
·(-![]() )=-1,∴x0=
)=-1,∴x0=![]() y0.①
y0.①
依题意,圆的方程为x2+y2=c2,
将①代入圆的方程得3![]() +
+![]() =c2,即y0=
=c2,即y0=![]() c,∴x0=
c,∴x0=![]() c,
c,
∴点A的坐标为![]() ,代入双曲线方程得
,代入双曲线方程得
![]() =1,即
=1,即![]() b2c2-
b2c2-![]() a2c2=a2b2,②
a2c2=a2b2,②
又∵a2+b2=c2,∴将b2=c2-a2代入②式,整理得![]() c4-2a2c2+a4=0,
c4-2a2c2+a4=0,
∴3![]() 4-8
4-8![]() 2+4=0,
2+4=0,
∴(3e2-2)(e2-2)=0,∵e>1,∴e=![]() ,
,
∴双曲线的离心率为![]() .
.

【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中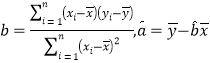 .
.