Question

【题目】已知曲线的极坐标方程是，以极点为原点，极轴为轴正方向建立平面直角坐标系，曲线的参数方程是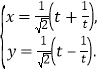（为参数）．

（Ⅰ）将曲线的参数方程化为普通方程；

（Ⅱ）求曲线与曲线交点的极坐标．

Answer 1

【答案】(Ⅰ)；(Ⅱ)与

【解析】试题分析：

（Ⅰ）将曲线的参数方程消去参数可得普通方程．（Ⅱ）方法一：把曲线的普通方程化为极坐标方程，然后结合消去，可得．进而可得所以，可得或，故可得交点的极坐标．方法二：将方程都化为直角坐标方程后，可求得曲线的交点坐标，然后再化成极坐标．

试题解析：

（Ⅰ）由曲线的参数方程得，

两式相乘可得曲线的普通方程为．

（Ⅱ）（方法一）将，代入曲线的普通方程，

得

由，得，

代入上式得，

解得，．

所以，解得或，

故所求交点的极坐标为与．

（方法二）由得，

故曲线的直角坐标为

解方程组，得或．

由得，，，故，因此对应点的极坐标为．

同理得对应点的极坐标为，

故所求交点的极坐标为与．