题目内容
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中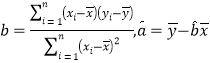 .
.
【答案】(1)206;(2)![]() .
.
【解析】试题分析:(1)先求出君子,代入公式求![]() ,
,![]() ,再求线性回归方程自变量为9的函数值,(2)先确定随机变量取法,在利用概率乘法求对应概率,列表可得分布列,根据数学期望公式求期望.
,再求线性回归方程自变量为9的函数值,(2)先确定随机变量取法,在利用概率乘法求对应概率,列表可得分布列,根据数学期望公式求期望.
试题解析:
(1)![]() ,经计算
,经计算![]() ,所以线性回归方程为
,所以线性回归方程为![]() ,
,
当![]() 时,
时,![]() 的估计值为206元;
的估计值为206元;
(2)![]() 的可能取值为0,300,500,600,800,1000;
的可能取值为0,300,500,600,800,1000;
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;
| 0 | 300 | 500 | 600 | 800 | 1000 |
|
|
|
|
|
|
|
所以![]() 的数学期望
的数学期望![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计数据表明,样本中所有人每天用于阅读的时间(简称阅读用时)都不超过3小时,其频数分布表如下:(用时单位:小时)
用时分组 |
|
|
|
|
|
|
频数 | 10 | 20 | 50 | 60 | 40 | 20 |
(1)用样本估计总体,求该市市民每天阅读用时的平均值;
(2)为引导市民积极参与阅读,有关部门牵头举办市读书经验交流会,从这200人中筛选出男女代表各3名,其中有2名男代表和1名女代表喜欢古典文学.现从这6名代表中任选2名男代表和2名女代表参加交流会,求参加交流会的4名代表中,喜欢古典文学的男代表多于喜欢古典文学的女代表的概率.
【题目】某食品集团生产的火腿按行业生产标准分成8个等级,等级系数![]() 依次为1,2,3,…,8,其中
依次为1,2,3,…,8,其中![]() 为标准
为标准![]() ,
, ![]() 为标准
为标准![]() .已知甲车间执行标准
.已知甲车间执行标准![]() ,乙车间执行标准
,乙车间执行标准![]() 生产该产品,且两个车间的产品都符合相应的执行标准.
生产该产品,且两个车间的产品都符合相应的执行标准.
(1)已知甲车间的等级系数![]() 的概率分布列如下表,若
的概率分布列如下表,若![]() 的数学期望E(X1)=6.4,求
的数学期望E(X1)=6.4,求![]() ,
, ![]() 的值;
的值;
X1 | 5 | 6 | 7 | 8 |
P | 0.2 |
|
|
|
(2)为了分析乙车间的等级系数![]() ,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
用该样本的频率分布估计总体,将频率视为概率,求等级系数![]() 的概率分布列和均值;
的概率分布列和均值;
(3)从乙车间中随机抽取5根火腿,利用(2)的结果推断恰好有三根火腿能达到标准![]() 的概率.
的概率.