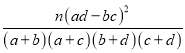题目内容
【题目】某市一批养殖专业户投资石金钱龟养殖业,行业协会为了了解市场行情,对石金钱龟幼苖销售价格进行调查。2017年12月随机抽取500户销售石金钱龟幼苖的平均价格,得到如下不完整的频率分布统计表:
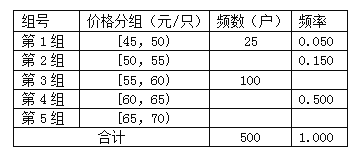
(Ⅰ)完成统计表。
(Ⅱ)为了向石金钱龟养殖户提供更好的幼苖销售参考,协会决定2018年1月份从第1,3,5组中用分层抽样方法取出7户出售幼龟价格跟踪调查,求第1,3,5组1月份接受调查的户数。
(Ⅲ)在(Ⅱ)的前提下,协会决定从选出的7个养殖户中随机抽取3户总结销售经验.为了鼓励养殖户支持调查工作,协会决定:发给第1组被抽到的每户幸运奖奖金210元,第3组被抽到的每户幸运奖奖金70元,第5组被抽到的每户幸运奖奖金140元.记发出的幸运奖总奖金额为![]() 元,求
元,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【答案】(1)见解析(2) 第1,3,5组接受调查的户数分别为1,4,2(3)见解析
【解析】【试题分析】(I)用![]() 乘以频率得到频数,由此填写好表格.(II)利用分层抽样各层的比例计算得每组抽取的人数.(III)
乘以频率得到频数,由此填写好表格.(II)利用分层抽样各层的比例计算得每组抽取的人数.(III)![]() 的所有可能取值为210,280,350,420,490.利用古典概型的计算公式计算出概率,并求出期望值.
的所有可能取值为210,280,350,420,490.利用古典概型的计算公式计算出概率,并求出期望值.
【试题解析】
(Ⅰ)

(Ⅱ)按分层抽样,可得第1组抽取的户数:![]() ,第3组抽取的户数:
,第3组抽取的户数:![]() ,第5组抽取的户数:
,第5组抽取的户数:![]() .
.
因此,第1,3,5组接受调查的户数分别为1,4,2
(Ⅲ)依题意,![]() 的所有可能取值为210,280,350,420,490,则
的所有可能取值为210,280,350,420,490,则
![]()
![]()
![]()
![]()
![]()
所以![]() 的分布列为:
的分布列为:

所以![]() 的数学期望为:
的数学期望为:![]()

【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
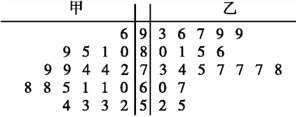
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
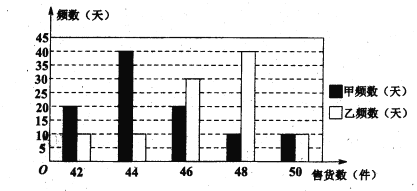
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 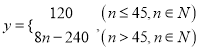
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
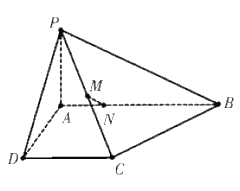
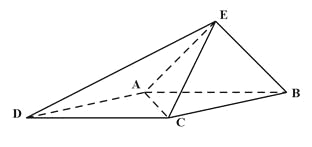
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
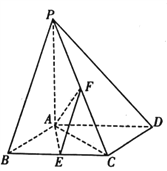
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了![]() 人,将调查情况进行整理后制成下表:
人,将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(![]() )完成被调查人员的频率分布直方图.
)完成被调查人员的频率分布直方图.
(![]() )若从年龄在
)若从年龄在![]() ,
,![]() 的被调查者中各随机选取
的被调查者中各随机选取![]() 人进行追踪调查,求恰有
人进行追踪调查,求恰有![]() 人不赞成的概率.
人不赞成的概率.
(![]() )在
)在![]() 在条件下,再记选中的
在条件下,再记选中的![]() 人中不赞成“车辆限行”的人数为
人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】某校推广新课改,在两个程度接近的班进行试验,一班为新课改班级,二班为非课改班级,经过一个学期的教学后对期末考试进行分析评价,规定:总分超过550(或等于550分)为优秀,550以下为非优秀,得到以下列联表:
优秀 | 非优秀 | 合计 | |
一班 | 35 | 13 | |
二班 | 25 | ||
合计 | 90 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否在犯错误的概率不超过0.005的前提下认为推广新课改与数学成绩有关系?
参考数据:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
k2=