题目内容
3.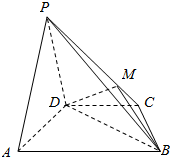 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)求三棱锥P-BCD的体积.
分析 (1)由线线垂直得到线面垂直推出面面垂直;(2)求出∠CDB的角度,求出PE的长,代入棱锥的体积公式即可.
解答 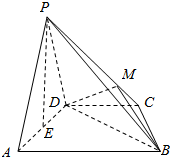 (1)证明:如图示:
(1)证明:如图示:
取AD中点E,连PE,因为△PAD是等边三角形
所以PE⊥AD.
又平面PAD⊥平面ABCD,且交线为AD.
所以PE⊥平面ABCD 所以PE⊥BD,
在△ABD中,AB=8,AD=4,BD=4$\sqrt{3}$
所以,AB2=AD2+BD2,即BD⊥AD,
PE∩AD=E,所以BD⊥平面PAD,
BD?面BDM,所以平面MBD⊥平面PAD;
(2)解:由(1)可知∠DAB=60°,AB∥DC,
所以∠CDB=30°,PE=$2\sqrt{3}$
$\begin{array}{l}{V_{P-BDC}}=\frac{1}{3}PE•{S_{△BDC}}=\frac{1}{3}×PE×\frac{1}{2}BD•DCsin∠BDC\\=\frac{1}{6}×2\sqrt{3}×4\sqrt{3}×4×\frac{1}{2}=8\end{array}$.
点评 本题考查了面面垂直的判定定理,考查柱、锥、台的体积,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.233除以9的余数是( )
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
11.{an}是首项a1=1,公差d=3的等差数列,若an=2014,则序号n的值为( )
| A. | 670 | B. | 672 | C. | 674 | D. | 668 |
13.圆C1:(x-3)2+y2=1,圆C2:(x+3)2+y2=4,若圆M与两圆均外切,则圆心M的轨迹是( )
| A. | 双曲线的一支 | B. | 一条直线 | C. | 椭圆 | D. | 双曲线 |