题目内容
14.已知定义域是R的偶函数f(x)在[0,+∞)上单调递增,若$x∈[{\frac{1}{2},1}]$时,f(1+xlog27•log7a)≤f(x-2)恒成立,则实数a的取值范围是[$\frac{1}{4}$,1].分析 f(x)是偶函数,且f(x)在[0,+∞)上是增函数,x∈[$\frac{1}{2}$,1]时,不等式f(1+xlog2a)≤f(x-2)恒成立,可得x∈[$\frac{1}{2}$,1]时,|1+xlog2a|≤2-x,化为$\frac{x-3}{x}$≤log2a≤$\frac{1-x}{x}$,x∈[$\frac{1}{2}$,1].再利用函数的单调性即可得出.
解答 解:∵f(x)是偶函数,且f(x)在[0,+∞)上是增函数,
x∈[$\frac{1}{2}$,1]时,不等式f(1+xlog2a)≤f(x-2)恒成立,
∴x∈[$\frac{1}{2}$,1]时,|1+xlog2a|≤2-x,
∴x-2≤1+xlog2a≤2-x,x∈[$\frac{1}{2}$,1].
∴$\frac{x-3}{x}$≤log2a≤$\frac{1-x}{x}$,x∈[$\frac{1}{2}$,1].
由$\frac{x-3}{x}$=1-$\frac{3}{x}$在x∈[$\frac{1}{2}$,1]的最大值为-2,
$\frac{1-x}{x}$=$\frac{1}{x}$-1在x∈[$\frac{1}{2}$,1]的最小值为0.
∴-2≤log2a≤0,
解得$\frac{1}{4}$≤a≤1.
故答案为:[$\frac{1}{4}$,1].
点评 本题考查了函数的奇偶性与单调性,属于中档题.

练习册系列答案
相关题目
4.“φ=π”是“函数f(x)=sin(x+φ)为奇函数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
4.下函数f(x)=2sin(2x+$\frac{π}{6}$),当x∈[$\frac{π}{12}$,$\frac{π}{2}$]时f(x)的值域为( )
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-1,1] | C. | [-$\frac{1}{2}$,1] | D. | [-1,2] |
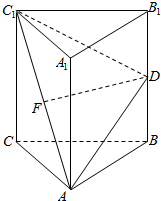 如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.
如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.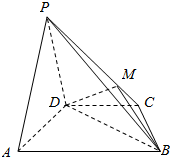 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.