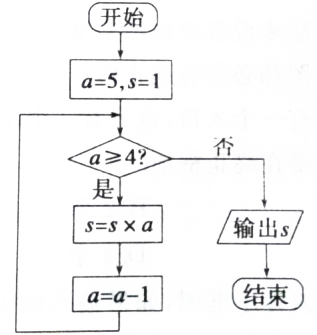
题目内容
18.已知在半径为8的圆O中,弦AB的长为8.(1)求弦AB所对的圆心角α(0<α<π)的大小.
(2)求α所在的扇形弧长l及弧所在的弓形的面积S.
分析 (1)由题意可得△OAB为等边三角形,可得α=$\frac{π}{3}$;
(2)由(1)和弧长公式可得l的值,而S=S扇形-S△OAB,由扇形和三角形的面积公式可得.
解答 解:(1)∵在半径为8的圆O中,弦AB的长为8,
∴△OAB为等边三角形,
∴弦AB所对的圆心角α=$\frac{π}{3}$;
(2)由(1)可得弧长l=8×$\frac{π}{3}$=$\frac{8π}{3}$,
弓形的面积S=S扇形-S△OAB=$\frac{1}{2}×\frac{8π}{3}×8$-$\frac{1}{2}×{8}^{2}×\frac{\sqrt{3}}{2}$=$\frac{32π}{3}$-16$\sqrt{3}$
点评 本题考查弧度制,涉及扇形和三角形的面积公式,属基础题.

练习册系列答案
相关题目
8.若f′(x0)=2,则$\underset{lim}{k→0}$$\frac{f({x}_{0}+k)-f({x}_{0})}{2k}$=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 无法确定 |
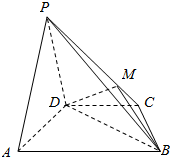 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.