题目内容
8.若过点A(0,-1)的直线l与曲线x2+(y-3)2=12有公共点,则直线l的斜率的取值范围为$({-∞,-\frac{{\sqrt{5}}}{5}}]∪[{\frac{{\sqrt{5}}}{5},+∞})$.分析 用代数法,先联立方程,消元后得到一个方程,再考虑二次项系数为0与不为0讨论,即可求得直线l的斜率的取值范围
解答 解:设直线方程为y=kx-1(k≠0),
根据题意:$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+(y-3)^{2}=12}\end{array}\right.$,
消去y整理得(1-k2)x2-8kx+4=0,
当1-k2=0即k=±1时,方程有解.
当1-k2≠0时,
∵△≥0,即64k2-16(1-k2)≥0,
∴k∈(-∞,-$\frac{\sqrt{5}}{5}$]∪[$\frac{\sqrt{5}}{5}$,+∞).
故答案是:$({-∞,-\frac{{\sqrt{5}}}{5}}]∪[{\frac{{\sqrt{5}}}{5},+∞})$.
点评 本题的考点是直线与圆的关系,主要考查直线与双曲线的位置关系,在只有一个公共点时,不要忽视了与渐近线平行的情况.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
16.已知角α终边上一点P(2,-$\sqrt{5}$),则sinα等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{\sqrt{5}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
20. 如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
 如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )| A. | AD+BC=2MN | B. | AD•BC=MN2 | C. | $\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{MN}$ | D. | MN=$\sqrt{\frac{A{D}^{2}+B{C}^{2}}{2}}$ |
18.若方程log2$\frac{{2}^{x}-1}{{2}^{x}+1}$=m在x∈[1,2]上有解,则实数m的取值范围为( )
| A. | [1,2] | B. | [log2$\frac{1}{3}$,log2$\frac{3}{5}$] | C. | [-∞,log2$\frac{1}{3}$] | D. | [log2$\frac{3}{5}$,+∞] |
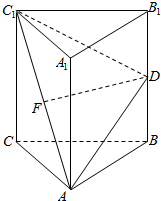 如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.
如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.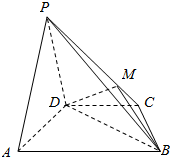 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.