题目内容
11.{an}是首项a1=1,公差d=3的等差数列,若an=2014,则序号n的值为( )| A. | 670 | B. | 672 | C. | 674 | D. | 668 |
分析 由等差数列的通项公式可得n的方程,解方程可得.
解答 解:由题意和等差数列的通项公式可得:
an=1+3(n-1)=2014,
解得n=672,
故选:B.
点评 本题考查等差数列的通项公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知角α终边上一点P(2,-$\sqrt{5}$),则sinα等于( )
| A. | -$\frac{2}{3}$ | B. | -$\frac{\sqrt{5}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
20. 如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
 如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )
如图梯形ABCD中,AD∥BC,对角线AC、BD交于点O,点M,N分别在两腰上,MN过点O,且MN∥AD,OM=ON,则AD,BC,MN满足的关系是( )| A. | AD+BC=2MN | B. | AD•BC=MN2 | C. | $\frac{1}{AD}$+$\frac{1}{BC}$=$\frac{2}{MN}$ | D. | MN=$\sqrt{\frac{A{D}^{2}+B{C}^{2}}{2}}$ |
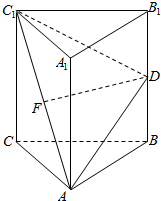 如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.
如图所示,棱柱ABC-A1B1C1为正三棱柱,且AC=C1C,其中点F,D分别为AC1,B1B的中点.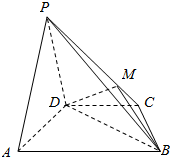 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AB=2CD=8.