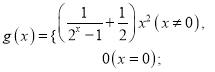题目内容
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)先利用勾股定理和线面垂直的性质得到线线垂直,再利用线面垂直的判定定理进行证明;(2)先利用前一步结论得到垂直关系,进而找出二面角的平面角,以垂直关系建立适当的空间直角坐标系,将线面角转化为空间向量进行求解.
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
又∵![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,∴
,∴![]()
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .(2)由(1)所证,
.(2)由(1)所证, ![]() 平面
平面![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() ,
,
而![]() ,所以
,所以![]() .
.
因为底面![]() 为平行四边形,
为平行四边形, ![]() ,
,
分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
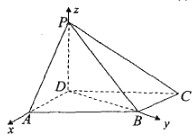
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则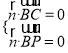 ,即
,即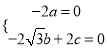 ,
,
令![]() ,则
,则![]()
∴![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为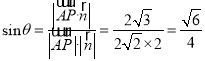 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:
算得,K2≈7.8.见附表:参照附表,得到的正确结论是( )
男 | 女 | 总计 | |||||
爱好 | 40 | 20 | 60 | ||||
不爱好 | 20 | 30 | 50 | ||||
总计 | 60 | 50 | 110 | ||||
P(K2≥k) | 0.050 | 0.010 | 0.001 | ||||
k | 3.841 | 6.635 | 10.828 | ||||
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”