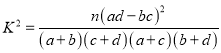题目内容
【题目】在极坐标系中,已知某曲线C的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求该曲线C的直角坐标系方程及离心率![]()
(2)已知点![]() 为曲线C上的动点,求点
为曲线C上的动点,求点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 知曲线C的极坐标方程为
知曲线C的极坐标方程为![]() 可化为直角坐标系方程
可化为直角坐标系方程![]() ,由于在椭圆方程中
,由于在椭圆方程中![]() ,故可求出离心率;(2)因为直线
,故可求出离心率;(2)因为直线![]() 的极坐标方程为
的极坐标方程为![]() ,所以直线
,所以直线![]() 的直角坐标系方程为
的直角坐标系方程为![]() ,方法一:因为曲线C的参数方程为
,方法一:因为曲线C的参数方程为![]() 为参数),所以可设点
为参数),所以可设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离为
的距离为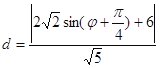 ,所以当
,所以当![]() ,即
,即![]() 时,
时,![]() .方法二:设与直线
.方法二:设与直线![]() 平行且与曲线C相切的直线为
平行且与曲线C相切的直线为![]() ,联立
,联立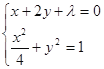 消去
消去![]() 整理得
整理得![]() ,令
,令![]() 得
得![]() ,当
,当![]() 时,切点
时,切点![]() 到直线
到直线![]() 的距离最大.
的距离最大.
试题解析:解:(1)由![]() 知曲线C的极坐标方程为
知曲线C的极坐标方程为![]() 可化为直角坐标系方程
可化为直角坐标系方程![]() 即
即![]() ..3分
..3分
由于在椭圆方程中![]() ..4分
..4分
故离心率![]() ..6分
..6分
(2)因为直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
所以直线![]() 的直角坐标系方程为
的直角坐标系方程为![]() ..8分
..8分
法一:因为曲线C的参数方程为![]() 为参数),所以可设点
为参数),所以可设点![]() 的坐标为
的坐标为![]() ..9分
..9分
则点![]() 到直线
到直线![]() 的距离为
的距离为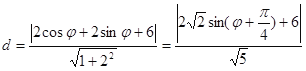 ..11分
..11分
所以当![]() ..12分
..12分
即![]() 时,
时,![]() ..13分
..13分
法二:设与直线![]() 平行且与曲线C相切的直线为
平行且与曲线C相切的直线为![]() ..8分
..8分
联立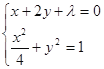 消去
消去![]() 整理得
整理得![]() ..10分
..10分
则![]() ,令
,令![]() 得
得![]() ..11分
..11分
当![]() 时,切点
时,切点![]() 到直线
到直线![]() 的距离最大为
的距离最大为![]() ..13分.
..13分.

【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查,调查问卷共10道题,答题情况如下表所示.
(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(2)从答对题目数小于8的出租车司机中任选出2人做进一步的调查,求选出的2人中至少有一名女出租车司机的概率.
答对题目数 | [0,8) | 8 | 9 | 10 |
女 | 2 | 13 | 12 | 8 |
男 | 3 | 37 | 16 | 9 |
【题目】高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:
喜欢中国古典文学 | 不喜欢中国古典文学 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢中国古典文学与性别有关?请说明理由;
的把握认为喜欢中国古典文学与性别有关?请说明理由;
(3)已知在喜欢中国古典文学的10位男生中,![]() ,
,![]() ,
,![]() 还喜欢数学,
还喜欢数学,![]() ,
,![]() 还喜欢绘画,
还喜欢绘画,![]() ,
,![]() 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求
还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |