题目内容
10.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,若点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$,则$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$(用向量$\overrightarrow{b}$、$\overrightarrow{c}$表示).分析 根据三角形法则,写出 $\overrightarrow{AD}$的表示式,根据点D的位置,得到 $\overrightarrow{BD}$与 $\overrightarrow{BC}$之间的关系,根据向量的减法运算,写出最后结果.
解答 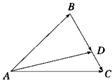 解:如图所示,在△ABC中,
解:如图所示,在△ABC中,
$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$
又$\overrightarrow{BD}$=2$\overrightarrow{DC}$,∴$\overrightarrow{BD}$=$\frac{2}{3}$$\overrightarrow{BC}$.
∵$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{c}$
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{BC}$=$\overrightarrow{c}$+$\frac{2}{3}$($\overrightarrow{b}$-$\overrightarrow{c}$)=$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$.
故答案为:$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$.
点评 本题考查向量的加减运算,考查三角形法则,是一个基础题,是解决其他问题的基础.

| A. | (-2,4) | B. | (2,-4) | C. | (1,-2) | D. | (-1,2) |
| A. | ±$\frac{\sqrt{10}}{5}$ | B. | ±$\frac{\sqrt{10}}{10}$ | C. | ±$\frac{1}{3}$ | D. | ±$\frac{1}{5}$ |
| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
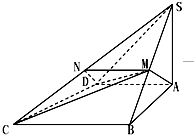 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.