题目内容
1.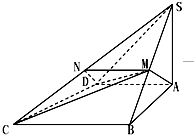 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.(1)求证:AM∥平面SDC;
(2)求三棱锥S-CDM的体积VS-CDM.
分析 (1)取SC中点N,连DN,MN,证明AM∥DN,然后利用直线与平面平行的判定定理证明AM∥平面SDC.
(2)解法(一)通过VS-CDM=VM-SCD=$\frac{1}{2}$VB-SCD=$\frac{1}{2}$VS-CDB求解即可.
解法(二):利用B到面CDM的距离是S到面CDM的距离相等,直接求解棱锥的体积即可.
解答 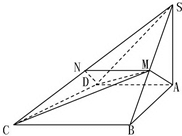 (1)证明:取SC中点N,连DN,MN可得,MN∥BC 且MN=$\frac{1}{2}$BC,
(1)证明:取SC中点N,连DN,MN可得,MN∥BC 且MN=$\frac{1}{2}$BC,
又AD∥BC 且AD=$\frac{1}{2}$BC,
所以,MN∥AD且MN=AD,
所以四边形AMND为平行四边形.…(3分)
那么,AM∥DN,
DN?平面ADC,
AM?平面ADC,…(5分)
所以,AM∥平面SDC.…(6分)
(2)解法(一):VS-CDM=VM-SCD=$\frac{1}{2}$VB-SCD=$\frac{1}{2}$VS-CDB=$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{2}$×4×4×4=$\frac{16}{3}$…(12分)
解法(二):
因为B到面CDM的距离是S到面CDM的距离相等,
所以VS-CDM=VB-CDM=VM-CDB=$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{2}$×4×4×4=$\frac{16}{3}$.…(12分)
点评 本题考查直线与平面平行的判定定理的应用,棱锥的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
11.已知焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{9}$=1的离心率是e=$\frac{1}{2}$,则a的值为( )
| A. | 3$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 12 |
9.设集合A={x|x2-x-2≤0},B={x|x≥a+1},若A?B,则a的取值范围是( )
| A. | a<2 | B. | a≥-2 | C. | a≤-2 | D. | a>2 |
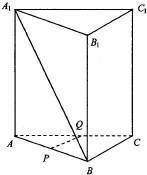 如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.
如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.