题目内容
20.从A,B,C,D,E5名学生中选出4名分别参加数学、物理、化学、外语竞赛,其中A不参加物理、化学竞赛,则不同的参赛方案种数为( )| A. | 24 | B. | 48 | C. | 72 | D. | 120 |
分析 根据题意,分2种情况讨论:①、A不参加任何竞赛,此时只需要将B、C、D、E四个人全排列,对应参加四科竞赛即可,由排列公式可得此时参赛方案的种数,②、A参加竞赛,依次分析A与其他四人的情况数目,由分步计数原理可得此时参赛方案的种数;进而由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、A不参加任何竞赛,
此时只需要将B、C、D、E四个人全排列,对应参加四科竞赛即可,有A44=24种参赛方案;
②、A参加竞赛,
此时A只能参加数学和外语竞赛,有2种情况,
在剩下的4人中任选3人,参加其他三科的竞赛,有A43=24种情况,
此时共有2×24=48种参赛方案;
综上,一共有24+48=72种参赛方案;
故选:C.
点评 本题考查排列组合的应用,此类问题一般优先分析“特殊”元素,即受到限制的元素.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
5.房山区某高中为了推进新课程改革,满足学生全面发展的需求,决定从高一年级开始,在每周的周一、周三、周五的格外活动期间同时开设信息技术、美术素描和音乐欣赏辅导讲座,每位同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
(1)求音乐欣赏辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
| 信息技术 | 美术素描 | 音乐欣赏 | |
| 周一 | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
| 周三 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{2}{3}$ |
| 周五 | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{2}{3}$ |
(2)设周三各辅导讲座满座的科目数为X,求随机变量X的分布列和数学期望.
12. 用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
 用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )| A. | $\sqrt{3}+1$ | B. | 1 | C. | $\sqrt{2}+1$ | D. | 3 |
9.已知复数z1=4-mi,z2=6m+ni,且m、n∈R,若z2=z12,则实数n=( )
| A. | -2,8 | B. | 2,-8 | C. | 64,-16 | D. | 16,-64 |
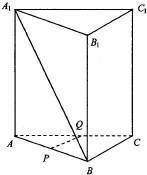 如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.
如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.