题目内容
2.在平面直角坐标系中,已知:A(3,0),B(0,4),O为坐标原点,以点P为圆心的圆P半径为1.①点P 坐标为P(1,2),试判断圆P与△OAB三边的交点个数;
②动点P在△OAB内运动,圆P与△OAB的三边有四个交点,求P点形成区域的面积.
分析 ①求出直线AB的方程,判断圆P与直线AB相交,点P坐标为P(1,2),圆P与OB相切,与OA相离,即可得出结论;
②取一个满足条件的圆,然后再找临界状况,第一种临界:与三边相切,即三角形内三条蓝色的直线;第二种临界:圆只与三角形的一个角相交,有两个顶点,即图内三个,
解答 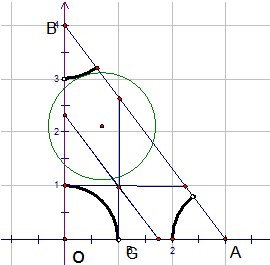 解:①直线AB的方程为4x+3y-12=0,P到AB的距离为$\frac{|4+6-12|}{5}$=$\frac{2}{5}$<1,
解:①直线AB的方程为4x+3y-12=0,P到AB的距离为$\frac{|4+6-12|}{5}$=$\frac{2}{5}$<1,
∴圆P与直线AB相交,
点P坐标为P(1,2),圆P与OB相切,与OA相离,
∴圆P与△OAB三边的交点个数为3个;
②直线AB的方程为4x+3y-12=0,当x=1时,y=$\frac{8}{3}$
这样上方的平行四边形的面积为$\frac{5}{3}$;
当y=1时,x=$\frac{9}{4}$,
这样右方的平行四边形的面积为$\frac{5}{4}$;
正方形面积为1,三个扇形正好为半径为1的半圆
∴最终结果为三个四边形面积之和减去半圆,
即面积为$\frac{47-6π}{12}$.
点评 本题考查直线与圆的位置关系,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
17.已知正四面体ABCD的棱长为1,O为底面BCD的中心,则$\overrightarrow{AB}•\overrightarrow{AO}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.设a∈[0,4],则使方程x2+ax+1=0有解的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
12. 用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
 用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )
用一个边长为2$\sqrt{2}$的正方形硬纸板,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为2的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为( )| A. | $\sqrt{3}+1$ | B. | 1 | C. | $\sqrt{2}+1$ | D. | 3 |
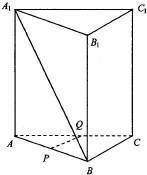 如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.
如图,侧棱与底面积垂直的三棱柱ABC-A1B1C1各侧棱和底面边长均为2,P,Q分别是棱AB、AC的中点,连结A1B.