题目内容
7. 已知椭圆C中心在坐标原点,对称轴为坐标轴,且过点A(2$\sqrt{6}$,2)、B(3,3).
已知椭圆C中心在坐标原点,对称轴为坐标轴,且过点A(2$\sqrt{6}$,2)、B(3,3).(Ⅰ) 求椭圆C的方程;
(Ⅱ)椭圆C上的任一点M(x1,y1),过原点O向半径为r的圆M作两条切线,是否存在r使得两条切线的斜率之积s为定值,若是,求出r,s值;若不是,请说明理由.
分析 (Ⅰ)设椭圆方程为mx2+ny2=1,点A(2$\sqrt{6}$,2)、B(3,3),代入$\left\{\begin{array}{l}{24m+4n=1}\\{9m+9n=1}\end{array}\right.$,求出m,n,即可
求椭圆C的方程;
(Ⅱ)设两条切线方程为y=k1x,y=k2x,由圆心到直线的距离等于半径,$\frac{|{k}_{1}{x}_{1}-{y}_{1}|}{\sqrt{1+{{k}_{1}}^{2}}}$=r,$\frac{|{k}_{2}{x}_{1}-{y}_{1}|}{\sqrt{1+{{k}_{2}}^{2}}}$=r,化简得k1,k2是方程(x12-r2)k2-2x1y1k+y12-r2=0的两个不相等的实数根,利用韦达定理,可得结论.
解答 解:(Ⅰ)设椭圆方程为mx2+ny2=1,
点A(2$\sqrt{6}$,2)、B(3,3),代入$\left\{\begin{array}{l}{24m+4n=1}\\{9m+9n=1}\end{array}\right.$,
∴m=$\frac{1}{36}$,n=$\frac{1}{12}$.
∴椭圆C的方程为$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{12}=1$;
(Ⅱ)斜率显然存在,设两条切线方程为y=k1x,y=k2x,
由圆心到直线的距离等于半径,$\frac{|{k}_{1}{x}_{1}-{y}_{1}|}{\sqrt{1+{{k}_{1}}^{2}}}$=r,$\frac{|{k}_{2}{x}_{1}-{y}_{1}|}{\sqrt{1+{{k}_{2}}^{2}}}$=r,
化简得k1,k2是方程(x12-r2)k2-2x1y1k+y12-r2=0的两个不相等的实数根,
∴k1k2=$\frac{{{y}_{1}}^{2}-{r}^{2}}{{{x}_{1}}^{2}-{r}^{2}}$=$\frac{-\frac{1}{3}{{x}_{1}}^{2}+12-{r}^{2}}{{{x}_{1}}^{2}-{r}^{2}}$=s,
∴s=-$\frac{1}{3}$,r=3.
点评 本题考查椭圆方程,考查直线与与圆的位置关系,考查待定系数法,考查学生的计算能力,属于中档题.

| A. | y=$\frac{1}{x}$ | B. | y=x3 | C. | y=sinx | D. | y=-3x |
| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |

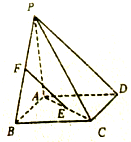 如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.
如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°. 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).