题目内容
14.在△ABC中,若S△ABC=12$\sqrt{3}$,ac=48,c-a=2,则b=2$\sqrt{13}$或$2\sqrt{37}$.分析 根据题意和三角形的面积公式分别求出角B、a、c的值,再分别由余弦定理求出边b的值.
解答 解:因为S△ABC=12$\sqrt{3}$,ac=48,
所以$\frac{1}{2}acsinB=12\sqrt{3}$,解得sinB=$\frac{\sqrt{3}}{2}$,
由0<B<π得,B=$\frac{π}{3}$或$\frac{2π}{3}$,
由$\left\{\begin{array}{l}{ac=48}\\{c-a=2}\end{array}\right.$得,c=8、a=6,
①当B=$\frac{π}{3}$时,由余弦定理得:b2=a2+c2-2accosB
=36+64-2×$48×\frac{1}{2}$=52,则b=2$\sqrt{13}$;
②当B=$\frac{2π}{3}$时,由余弦定理得:b2=a2+c2-2accosB
=36+64-2×$48×(-\frac{1}{2})$=148,则b=$2\sqrt{37}$,
综上可得,b的值是2$\sqrt{13}$或$2\sqrt{37}$,
故答案为:2$\sqrt{13}$或$2\sqrt{37}$.
点评 本题考查了余弦定理,以及三角形的面积公式,注意三角形内角的范围,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
19.设随机变量X:B(6,$\frac{1}{3}$),则D(X)等于( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{3}$ |
6.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=$\frac{1}{x}$ | B. | y=x3 | C. | y=sinx | D. | y=-3x |
3.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π),则函数f(x)的各极小值之和为( )
| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |
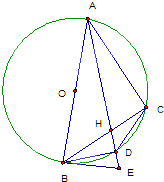 如图,圆O的直径AB、BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
如图,圆O的直径AB、BE为圆O的切线,点C为圆O上不同于A、B的一点,AD为∠BAC的平分线,且分别与BC交于H,与圆O交于D,与BE交于E,连结BD、CD.
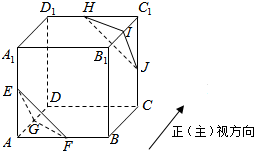 已知正方体ABCD-A1B1C1D1的棱长为2,点E,F,G,H,I,J分别是该正方体的棱AA1,AB,AD,C1D1,C1B1,C1C的中点,现从该正方体中截去棱锥A-EFG与棱锥C1-HIJ,若正(主)视方向如图所示,则剩余部分的几何体的侧(左)视图为( )
已知正方体ABCD-A1B1C1D1的棱长为2,点E,F,G,H,I,J分别是该正方体的棱AA1,AB,AD,C1D1,C1B1,C1C的中点,现从该正方体中截去棱锥A-EFG与棱锥C1-HIJ,若正(主)视方向如图所示,则剩余部分的几何体的侧(左)视图为( )