��Ŀ����
5�� ����Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��y��0��$�Ͱ�Բx2+y2=b2��y��0���������C������a��b��0����ͼ��ʾ������C��x����A��B���㣬��y�Ḻ�����ڵ�G����Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$��������Ϊ$\frac{{\sqrt{2}}}{2}$��F������һ�����㣬��P������Cλ��x���Ϸ�������һ�㣬�ҡ�PFG���ܳ���$2\sqrt{2}+2$��
����Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��y��0��$�Ͱ�Բx2+y2=b2��y��0���������C������a��b��0����ͼ��ʾ������C��x����A��B���㣬��y�Ḻ�����ڵ�G����Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$��������Ϊ$\frac{{\sqrt{2}}}{2}$��F������һ�����㣬��P������Cλ��x���Ϸ�������һ�㣬�ҡ�PFG���ܳ���$2\sqrt{2}+2$��������a��b��ֵ��
������M�ǰ�Բx2+y2=b2��y��0����A��B������һ�㣬C��-b��a����D��b��a��������MC��MD�ֱ�AB�ڵ�E��F����|AE|2+|BF|2��ȡֵ��Χ��
���� ����������Բ�������ʹ�ʽ��a��b��c�Ĺ�ϵ���ɵ�b=c������GΪ��Բ�Ľ��㣬����Բ�Ķ��壬�ɵ�a=2��b=1��
�����ɣ���֪��C��-1��$\sqrt{2}$����D��1��$\sqrt{2}$������M��cos�ȣ�sin�ȣ����ȡʣ��У�2�У�����ֱ��AC���̿ɵ�E��F�����꣬��������ľ��빫ʽ��������Ǻ����ĺ�ȱ任�����Һ����ĵ����ԣ����ɵõ�ȡֵ��Χ��
��� �⣺������Բ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$��������Ϊ$\frac{{\sqrt{2}}}{2}$������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��
��a2-b2=c2���ɵ�b=c��
��GΪ��Բ��һ�����㣬����F��0��c����G��0��-c����
����Բ�Ķ���ɵá�PFG���ܳ�Ϊ2a+2c=2$\sqrt{2}$+2��
���a=2��b=1��
�����ɣ���֪��C��-1��$\sqrt{2}$����D��1��$\sqrt{2}$����
��M��cos�ȣ�sin�ȣ����ȡʣ��У�2�У���
��ֱ��AC��y-$\sqrt{2}$=$\frac{sin��-\sqrt{2}}{cos��+1}$��x+1����
��y=0���ɵ�E��$\frac{-\sqrt{2}cos��-sin��}{sin��-\sqrt{2}}$��0����
ͬ�����F��$\frac{-\sqrt{2}cos��+sin��}{sin��-\sqrt{2}}$��0����
|AE|2+|BF|2=��$\frac{-\sqrt{2}��cos��+1��}{sin��-\sqrt{2}}$��2+��$\frac{\sqrt{2}��cos��-1��}{sin��-\sqrt{2}}$��2=$\frac{2��2co{s}^{2}��+2��}{��sin��-\sqrt{2}��^{2}}$=$\frac{4��2-si{n}^{2}�ȣ�}{��sin��-\sqrt{2}��^{2}}$
=4•$\frac{\sqrt{2}+sin��}{\sqrt{2}-sin��}$=-4��1+$\frac{2\sqrt{2}}{sin��-\sqrt{2}}$����
��u=sin�ȡ�[-1��0]��
|AE|2+|BF|2=-4��1+$\frac{2\sqrt{2}}{u-\sqrt{2}}$����[-1��0]�ϵĵ�����������
��|AE|2+|BF|2=��[12-8$\sqrt{2}$��4��������
���� ���⿼����Բ��Բ�Ķ���ͷ��̵����ã���Ҫ������Բ�Ķ����Բ�IJ������̵����ã��������Ǻ����ĺ�ȱ任��ʽ�����ú����Һ����ĵ����Ե����ã������е��⣮

 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�| A�� | -$\frac{{e}^{2��}��1-{e}^{2015��}��}{1-{e}^{2��}}$ | B�� | -$\frac{{e}^{2��}��1-{e}^{2015�У�}}{1-{e}^{��}}$ | ||
| C�� | -$\frac{1-{e}^{2016��}}{1-{e}^{2��}}$ | D�� | -$\frac{{e}^{2��}��1-{e}^{2014��}��}{1-{e}^{2��}}$ |
| A�� | 2-i | B�� | 2+i | C�� | 5-i | D�� | 5+i |
 ��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$���ҹ��㣨$\sqrt{3}$��$\frac{1}{2}$����
��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$���ҹ��㣨$\sqrt{3}$��$\frac{1}{2}$���� ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{5}}{5}$�����᳤Ϊ4��F1��F2Ϊ��Բ���ҽ��㣬��BΪ�¶��㣮
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{5}}{5}$�����᳤Ϊ4��F1��F2Ϊ��Բ���ҽ��㣬��BΪ�¶��㣮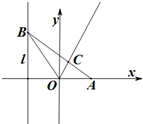 ��ͼ����֪����A��1��0������B�Ƕ�ֱ��l��x=-1�ϵĶ��㣬��BOA�Ľ�ƽ���߽�AB��C��
��ͼ����֪����A��1��0������B�Ƕ�ֱ��l��x=-1�ϵĶ��㣬��BOA�Ľ�ƽ���߽�AB��C�� ��ͼ����ֱ֪��l��������x2=4y�����ڵ�P��2��1��������x�ύ�ڵ�A������B������Ϊ��2��0����
��ͼ����ֱ֪��l��������x2=4y�����ڵ�P��2��1��������x�ύ�ڵ�A������B������Ϊ��2��0����