题目内容
【题目】闽越水镇是闽侯县打造闽都水乡文化特色小镇核心区，该小镇有一块1800平方米的矩形地块，开发商准备在中间挖出三个矩形池塘养闽侯特色金鱼，挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植柳树，形成柳中观鱼特色景观．假设池塘周围的基围宽均为2米，如图，设池塘所占的总面积为
平方米．
(1)试用
表示a及；
(2)当取何值时，才能使得最大？并求出的最大值．
【答案】（1）
，
；（2）当x为45米时，S最大，且S最大值为1 352平方米．
【解析】
(1)由题意结合边长关系确定a,S关于x的函数关系即可，注意实际问题中函数的定义域；
(2)由题意结合均值不等式的结论确定S取得最大值时x的值和S的最大值即可.
(1)由题图形知，3a＋6＝x，
∴
.
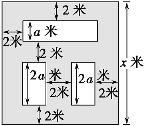
则总面积S＝
·a＋2a
＝a
＝
＝1 832－
，
即
．
(2)由S＝1 832－，
得S≤1 832－2
＝1 832－2×240＝1 352(平方米)．
当且仅当
＝
，此时，x＝45.
即当x为45米时，S最大，且S最大值为1 352平方米．
练习册系列答案
相关题目
