题目内容
4.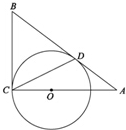 如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.求证:AC=2AD.
分析 证明Rt△ADO∽Rt△ACB,可得$\frac{BC}{OD}=\frac{AC}{AD}$,结合BC=2OC=2OD,即可证明结论.
解答 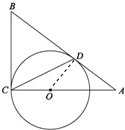 证明:连接OD.
证明:连接OD.
因为AB和BC分别与圆O相切于点D,C,所以ADO=∠ACB=90°
又因为∠A=∠A,所以Rt△ADO∽Rt△ACB,
所以$\frac{BC}{OD}=\frac{AC}{AD}$,
因为BC=2OC=2OD.
所以AC=2AD.
点评 本题考查圆的切线,考查三角形相似的判定与性质,比较基础.

练习册系列答案
相关题目
12.在区间[0,1]上随机取两个数x,y,记p1为事件“x+y≤$\frac{1}{2}$”的概率,P2为事件“xy≤$\frac{1}{2}$”的概率,则( )
| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
19.某同学将“五点法”画函数f(x)=Asin(wx+φ)(w>0,|φ|<$\frac{π}{2}$)在某一个时期内的图象时,列表并填入部分数据,如下表:
(1)请将上述数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平移$\frac{π}{6}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
| wx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(wx+φ) | 0 | 5 | -5 | 0 |
(2)将y=f(x)图象上所有点向左平移$\frac{π}{6}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
9.过三点A(1,0),B(0,$\sqrt{3}$),C(2,$\sqrt{3}$)则△ABC外接圆的圆心到原点的距离为( )
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{21}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $\frac{4}{3}$ |
16.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表
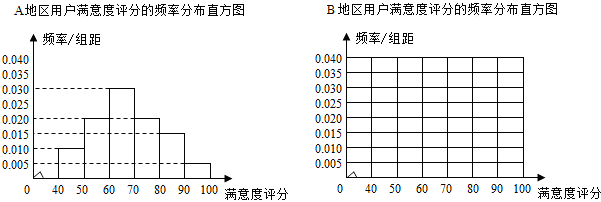
B地区用户满意度评分的频数分布表
(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:
估计哪个地区用户的满意度等级为不满意的概率大?说明理由.

B地区用户满意度评分的频数分布表
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 2 | 8 | 14 | 10 | 6 |
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
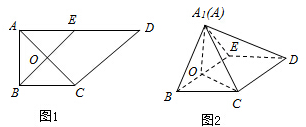 如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.