题目内容
13.已知数列{an}满足an+2=qan(q为实数,且q≠1),n∈N*,a1=1,a2=2,且a2+a3,a3+a4,a4+a5成等差数列(1)求q的值和{an}的通项公式;
(2)设bn=$\frac{{{{log}_2}{a_{2n}}}}{{{a_{2n-1}}}}$,n∈N*,求数列{bn}的前n项和.
分析 (1)通过an+2=qan、a1、a2,可得a3、a5、a4,利用a2+a3,a3+a4,a4+a5成等差数列,计算即可;
(2)通过(1)知bn=$\frac{n}{{2}^{n-1}}$,n∈N*,写出数列{bn}的前n项和Tn、2Tn的表达式,利用错位相减法及等比数列的求和公式,计算即可.
解答 解:(1)∵an+2=qan(q为实数,且q≠1),n∈N*,a1=1,a2=2,
∴a3=q,a5=q2,a4=2q,
又∵a2+a3,a3+a4,a4+a5成等差数列,
∴2×3q=2+3q+q2,
即q2-3q+2=0,
解得q=2或q=1(舍),
∴an=$\left\{\begin{array}{l}{{2}^{\frac{n-1}{2}},}&{n为奇数}\\{{2}^{\frac{n}{2}},}&{n为偶数}\end{array}\right.$;
(2)由(1)知bn=$\frac{{{{log}_2}{a_{2n}}}}{{{a_{2n-1}}}}$=$\frac{lo{g}_{2}{2}^{n}}{{2}^{n-1}}$=$\frac{n}{{2}^{n-1}}$,n∈N*,
记数列{bn}的前n项和为Tn,
则Tn=1+2•$\frac{1}{2}$+3•$\frac{1}{{2}^{2}}$+4•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n-2}}$+n•$\frac{1}{{2}^{n-1}}$,
∴2Tn=2+2+3•$\frac{1}{2}$+4•$\frac{1}{{2}^{2}}$+5•$\frac{1}{{2}^{3}}$+…+(n-1)•$\frac{1}{{2}^{n-3}}$+n•$\frac{1}{{2}^{n-2}}$,
两式相减,得Tn=3+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n-2}}$-n•$\frac{1}{{2}^{n-1}}$
=3+$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n-2}]}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n-1}}$
=3+1-$\frac{1}{{2}^{n-2}}$-n•$\frac{1}{{2}^{n-1}}$
=4-$\frac{n+2}{{2}^{n-1}}$.
点评 本题考查求数列的通项与前n项和,考查分类讨论的思想,利用错位相减法是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | 3 | B. | 4 | C. | 18 | D. | 40 |
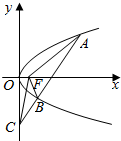 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )| A. | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B. | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C. | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D. | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |
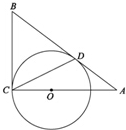 如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.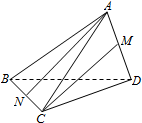 如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.
如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.