题目内容
19.某同学将“五点法”画函数f(x)=Asin(wx+φ)(w>0,|φ|<$\frac{π}{2}$)在某一个时期内的图象时,列表并填入部分数据,如下表:| wx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(wx+φ) | 0 | 5 | -5 | 0 |
(2)将y=f(x)图象上所有点向左平移$\frac{π}{6}$个单位长度,得到y=g(x)图象,求y=g(x)的图象离原点O最近的对称中心.
分析 (1)由五点作图法即可将数据补充完整,写出函数的解析式;
(2)由函数y=Asin(ωx+φ)的图象变换可得g(x),解得其对称中心即可得解.
解答 解:(1)数据补充完整如下表:
| wx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | $\frac{13π}{12}$ |
| Asin(wx+φ) | 0 | 5 | 0 | -5 | 0 |
(2)将y=f(x)图象上所有点向左平移$\frac{π}{6}$个单位长度,得到y=g(x)=5sin[2(x+$\frac{π}{6}$)-$\frac{π}{6}$]=5sin(2x+$\frac{π}{6}$).
由2x+$\frac{π}{6}$=kπ,k∈Z,可解得:x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,
当k=0时,可得:x=-$\frac{π}{12}$.
从而可得离原点O最近的对称中心为:(-$\frac{π}{12}$,0).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.根据如图框图,当输入x为2006时,输出的y=( )
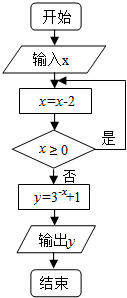

| A. | 2 | B. | 4 | C. | 10 | D. | 28 |
7.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 134石 | B. | 169石 | C. | 338石 | D. | 1365石 |
14.已知集合A={(x,y)|x2+y2≤1,x,y∈Z},B={(x,y)||x|≤2,|y|≤2,x,y∈Z},定义集合A⊕B={(x1+x2,y1+y2)|(x1,y1)∈A,(x2,y2)∈B},则A⊕B中元素的个数为( )
| A. | 77 | B. | 49 | C. | 45 | D. | 30 |
11.已知等比数列{an}满足a1=$\frac{1}{4}$,a3a5=4(a4-1),则a2=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
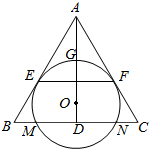 如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.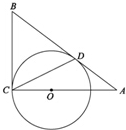 如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC. 如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.