题目内容
4.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2.(1)若点A(0,b)与焦点F1、F2构成△AF1F2为等腰直角三角形,求椭圆的离心率.
(2)若椭圆E的离心率为$\frac{1}{2}$,过点P(0,1)的直线与椭圆交于B、C两点,且当点B、C关于y轴对称时,|BC|=$\frac{{4\sqrt{6}}}{3}$,求椭圆E的方程.
分析 (1)由题意可得c=b,由a,b,c的关系和离心率公式,计算即可得到;
(2)由离心率为$\frac{1}{2}$,可得3a2=4b2,①,再由B,C关于y轴对称,可得它们的纵坐标为1,代入椭圆方程,结合条件可得a,b的方程,解方程,即可得到a2=4,b2=3,则椭圆方程可得.
解答 解:(1)△AF1F2为等腰直角三角形,
则|OA|=|OF1|,即b=c,
c=$\sqrt{{a}^{2}-{b}^{2}}$,即有c=$\frac{\sqrt{2}}{2}$a,
e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
(2)由e=$\frac{c}{a}$=$\frac{1}{2}$,可得a2=4c2=4(a2-b2),
即3a2=4b2,①
由B,C关于y轴对称,设B(m,n),C(-m,n),
|BC|=2|m|,又P为BC的中点,则2n=2,即n=1,
由$\frac{{m}^{2}}{{a}^{2}}$+$\frac{{n}^{2}}{{b}^{2}}$=1可得|m|=$\frac{a}{b}$$\sqrt{{b}^{2}-1}$,
由题意可得$\frac{2a}{b}$$\sqrt{{b}^{2}-1}$=$\frac{4\sqrt{6}}{3}$,②
由①②解得a2=4,b2=3,
则椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率的运用和方程的运用,注意点在椭圆上满足椭圆方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
15.甲、乙两同学的6次考试成绩分别为:
(Ⅰ)画出甲、乙两同学6次考试成绩的茎叶图;
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
| 甲 | 99 | 89 | 97 | 85 | 95 | 99 |
| 乙 | 89 | 93 | 90 | 89 | 92 | 90 |
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
12.四边形ABCD中,AB=BC,AD⊥DC,AC=1,∠ACD=θ,若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$,则cos2θ等于( )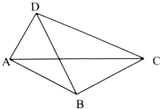

| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
4.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算K2≈0.99,根据这一数据分析,下列说法正确的是( )
| A. | 有99%的人认为该栏目优秀 | |
| B. | 有99%的人认为该栏目是否优秀与改革有关系 | |
| C. | 有99%的把握认为电视栏目是否优秀与改革有关系 | |
| D. | 没有理由认为电视栏目是否优秀与改革有关系 |
9.$\int_0^1{({e^x}+2x)dx=}$( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
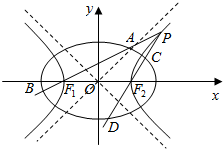 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.