题目内容
7.若数列{an},{bn}的通项公式分别是${a_n}={(-1)^{n+2014}}a$,${b_n}=2+\frac{{{{(-1)}^{n+2015}}}}{n}$,且an<bn对任意n∈N*恒成立,则实数a的取值范围是( )| A. | [-1,$\frac{1}{2}$) | B. | [-2,$\frac{1}{2}$) | C. | [-2,$\frac{3}{2}$) | D. | [-1,$\frac{3}{2}$) |
分析 an<bn对任意n∈N*恒成立,分类讨论:当n为偶数时,可得a<2-$\frac{1}{n}$$<2-\frac{1}{2}$,解得a范围.当n为奇数时,可得-a<2+$\frac{1}{n}$,解得a范围,求其交集即可.
解答 解:∵an<bn对任意n∈N*恒成立,
∴当n为偶数时,可得a<2-$\frac{1}{n}$$<2-\frac{1}{2}$,解得$a<\frac{3}{2}$.
当n为奇数时,可得-a<2+$\frac{1}{n}$,解得$a>-(2+\frac{1}{n})$.∴a≥-2.
∴$-2≤a<\frac{3}{2}$.
故选:C.
点评 本题考查了数列的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.若满足条件AB=2且B=60°的三角形有两个,则AC边长的取值范围是( )
| A. | (1,2) | B. | ($\sqrt{2}$,$\sqrt{3}$) | C. | ($\sqrt{3}$,2) | D. | ($\sqrt{2}$,2) |
15.甲、乙两同学的6次考试成绩分别为:
(Ⅰ)画出甲、乙两同学6次考试成绩的茎叶图;
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
| 甲 | 99 | 89 | 97 | 85 | 95 | 99 |
| 乙 | 89 | 93 | 90 | 89 | 92 | 90 |
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
2.设f,g都是X到Y的映射,其中X={0,1,2,3},Y={0,1,2,3}其对应法则(从上到下)如下表
设a=g[f(3)],b=g[g(2)],c=f{g[f(1)]},则a,b,c的大小关系为( )
| x | 0 | 1 | 2 | 3 |
| y=f(x) | 3 | 0 | 1 | 2 |
| x | 0 | 1 | 2 | 3 |
| y=g(x) | 1 | 0 | 3 | 2 |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
12.四边形ABCD中,AB=BC,AD⊥DC,AC=1,∠ACD=θ,若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$,则cos2θ等于( )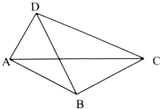

| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
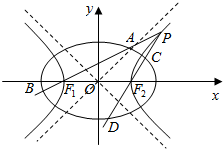 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),以该椭圆上的异于长轴端点的点和椭圆的左,右焦点F1,F2为顶点的三角形的周长为8$\sqrt{2}$,以椭圆的四个顶点组成的菱形的面积为8$\sqrt{2}$,双曲线G:x2-y2=m(m>0)的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A,B和C,D.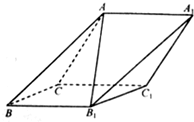 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.