题目内容
17.已知函数f(x)=lnx+$\frac{{x}^{2}}{2}$+2kx,其中常数k∈R.(1)求f(x)的单调增区间;
(2)若y=f(x)有两个极值点x1,x2,证明f(x2)<-$\frac{3}{2}$.
分析 (1)先求出函数f(x)的导数,通过讨论k的范围,从而得到函数的递增区间;
(2)由(1)得k>1时,得:x2-2kx+1=0,在x>0时有两个零点,根据根与系数的关系,得:f(x2)=lnx2-$\frac{{{x}_{2}}^{2}}{2}$-1,通过讨论其单调性,从而得到结论.
解答 解:(1)f′(x)=$\frac{1}{x}$+x-2k=$\frac{{x}^{2}-2kx+1}{x}$(x>0),
①当k≤1时,f′(x)≥2$\sqrt{\frac{1}{x}•x}$-2k=2-2k≥0,
∴函数f(x)为增函数.
②当k>1时,由f′(x)=0 得:x2-2kx+1=0,解得两根:x1,x2,
其中0<x1=k-$\sqrt{{k}^{2}-1}$<x2=k+$\sqrt{{k}^{2}-1}$,
x,f′(x),f(x)的取值变化情况如下表:
| x | (0,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
当k>1时,f(x)的增区间为(0,k-$\sqrt{{k}^{2}-1}$],[k+$\sqrt{{k}^{2}-1}$,+∞);
(2)当k≤1时,y=f(x)在(0,+∞)上是增函数,至多有一极值点,不合题意.
当k>1时,令f′(x)=0,得:x2-2kx+1=0,
在x>0时有两个零点,则x1+x2=2k,x1•x2=1,
f(x2)=lnx2+$\frac{{{x}_{2}}^{2}}{2}$-2kx2=lnx2+$\frac{{{x}_{2}}^{2}}{2}$-($\frac{1}{{x}_{2}}$+x2)x2,
f(x2)=lnx2-$\frac{{{x}_{2}}^{2}}{2}$-1,
f′(x2)=$\frac{1}{{x}_{2}}$-x2=$\frac{(1{-x}_{2})(1{+x}_{2})}{{x}_{2}}$,
当x2∈(0,1)时,f′(x2)>0,当x∈(1,+∞)时,f′(x2)<0,
∴f(x2)<f(1)=-$\frac{3}{2}$.
点评 本题考察了函数的单调性,考察导数的应用,考察根与系数的关系,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.四边形ABCD中,AB=BC,AD⊥DC,AC=1,∠ACD=θ,若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$,则cos2θ等于( )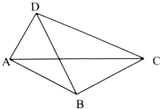

| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
2.命题“?x0∈(0,+∞),2x0<x02”的否定为( )
| A. | ?x∈(0,+∞),2x<x2 | B. | ?x∈(0,+∞),2x>x2 | C. | ?x∈(0,+∞),2x≥x2 | D. | ?x∈(0,+∞),2x≥x2 |
9.$\int_0^1{({e^x}+2x)dx=}$( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
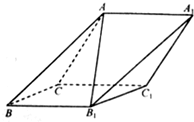 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.