题目内容
20．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的函数是（ ）| A． | y=x+x-1 | B． | y=x3+x | C． | y=2x+log2x | D． | $y={x^{\frac{1}{2}}}$ |
分析 根据函数奇偶数和单调性的性质分别进行判断即可．
解答 解：A．y=x+x-1是奇函数，在区间（0，+∞）不是单调函数，
B．y=x3+x是奇函数，函数的导数y′=3x2+1＞0，则函数为增函数，满足条件．
C．y=2x+log2x在（0，+∞）上为增函数，为非奇非偶函数．
D.$y={x^{\frac{1}{2}}}$在[0，+∞）上为增函数，但函数为非奇非偶函数，
故满足条件的是B，
故选：B
点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，双曲线的一个焦点在直线l上，则双曲线的方程为（ ）
| A． | $\frac{{3{x^2}}}{25}-\frac{{3{y^2}}}{100}=1$ | B． | $\frac{{3{x^2}}}{100}-\frac{{3{y^2}}}{25}=1$ | ||
| C． | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | D． | $\frac{x^2}{5}-\frac{y^2}{20}=1$ |
8．运行如图所示的程序框图，若输出的结果是36，则输入的n=（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
15．甲、乙两同学的6次考试成绩分别为：
（Ⅰ）画出甲、乙两同学6次考试成绩的茎叶图；
（Ⅱ）计算甲、乙两同学考试成绩的方差，并对甲、乙两同学的考试成绩做出合理评价．
| 甲 | 99 | 89 | 97 | 85 | 95 | 99 |
| 乙 | 89 | 93 | 90 | 89 | 92 | 90 |
（Ⅱ）计算甲、乙两同学考试成绩的方差，并对甲、乙两同学的考试成绩做出合理评价．
过⊙O外一点P作⊙O的切线PA，切点为A，连OP与⊙O交于点C，过C作AP的垂线，垂足为D，若PA=8cm，PC=4cm，则PD的长为3.2．
12．四边形ABCD中，AB=BC，AD⊥DC，AC=1，∠ACD=θ，若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$，则cos2θ等于（ ）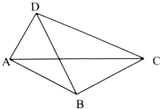
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
4．为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了100位居民进行调查，经过计算K2≈0.99，根据这一数据分析，下列说法正确的是（ ）
| A． | 有99%的人认为该栏目优秀 | |
| B． | 有99%的人认为该栏目是否优秀与改革有关系 | |
| C． | 有99%的把握认为电视栏目是否优秀与改革有关系 | |
| D． | 没有理由认为电视栏目是否优秀与改革有关系 |