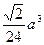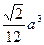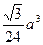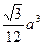题目内容
(本小题满分14分)
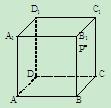
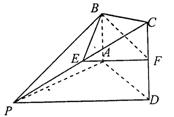
如图,在四棱锥P—ABCD中,AB∥CD,CD=2AB,AB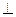 平面PAD,E为PC的中点.
平面PAD,E为PC的中点.
(1)求证:BE∥平面PAD;
(2)若AD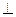 PB,求证:PA
PB,求证:PA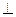 平面ABC D.
平面ABC D.
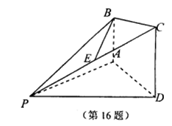
如图,在四棱锥P—ABCD中,AB∥CD,CD=2AB,AB
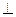 平面PAD,E为PC的中点.
平面PAD,E为PC的中点.(1)求证:BE∥平面PAD;
(2)若AD
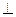 PB,求证:PA
PB,求证:PA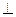 平面ABC D.
平面ABC D.
略
证明:(1)(方法一)取PD中点F,连结EF,AF.
因为E是PC的中点,F是PD的中点,
所以EF∥CD,且CD=2EF.
又因为AB∥CD,CD=2 AB,所以EF=AB,即四边形ABEF是平行四边形.
AB,所以EF=AB,即四边形ABEF是平行四边形.
因此BE∥AF.………………5分
又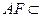 平面PAD,
平面PAD,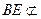 平面PAD,
平面PAD,
所以BE∥平面PAD.………………8分
(方法二)延长DA、CB,交于点F,连结PF.
因为AB∥CD,CD=2AB,
所以B为CF的中点.
又因为E为PC的中点,
所以BE∥PF.………………5分
因为 平面PAD,
平面PAD,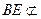 平面PAD,
平面PAD,
所以BE∥平面PAD.………………8分
(方法三)取CD中点F,连结EF,BF.
 因为E为PC中点,
因为E为PC中点, F为CD中点,
F为CD中点,
所以EF∥PD.
因为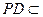 平面PAD,
平面PAD,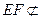
 平面PAD,
平面PAD,
所以EF∥平面PA D.………………2分
因为F为CD中点,所以CD=2FD.
又CD=2AB,AB∥CD,故AB=FD,即四边形ABFD为平行四边形,所以BF∥AD.
因为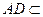 平面PAD,
平面PAD,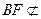 平面PAD,所以BF∥平
平面PAD,所以BF∥平 面PAD.
面PAD.
因为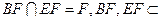 平面BEF,
平面BEF,
所以平面BEF∥平面PA D.………………6分
因为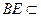 平面BEF,所以BE∥平面PA D.………………8分
平面BEF,所以BE∥平面PA D.………………8分
(2)因为AB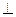 平面PAD,PA,
平面PAD,PA,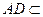 平面PAD,
平面PAD,
所以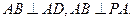 ……………………10分
……………………10分
因为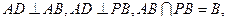
所以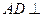 平面PA B.………
平面PA B.……… ………12分
………12分
又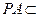 平面PAB,所以
平面PAB,所以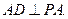
因为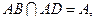 故PA
故PA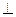 面ABCD.……………………14分
面ABCD.……………………14分
因为E是PC的中点,F是PD的中点,
所以EF∥CD,且CD=2EF.
|
 AB,所以EF=AB,即四边形ABEF是平行四边形.
AB,所以EF=AB,即四边形ABEF是平行四边形.因此BE∥AF.………………5分
又
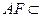 平面PAD,
平面PAD,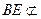 平面PAD,
平面PAD,所以BE∥平面PAD.………………8分
(方法二)延长DA、CB,交于点F,连结PF.
因为AB∥CD,CD=2AB,
所以B为CF的中点.
又因为E为PC的中点,
所以BE∥PF.………………5分
因为
 平面PAD,
平面PAD,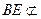 平面PAD,
平面PAD,所以BE∥平面PAD.………………8分
(方法三)取CD中点F,连结EF,BF.
 因为E为PC中点,
因为E为PC中点, F为CD中点,
F为CD中点,所以EF∥PD.
因为
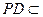 平面PAD,
平面PAD,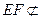
 平面PAD,
平面PAD,所以EF∥平面PA D.………………2分
因为F为CD中点,所以CD=2FD.
|
因为
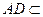 平面PAD,
平面PAD,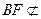 平面PAD,所以BF∥平
平面PAD,所以BF∥平 面PAD.
面PAD.因为
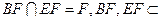 平面BEF,
平面BEF,所以平面BEF∥平面PA D.………………6分
因为
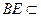 平面BEF,所以BE∥平面PA D.………………8分
平面BEF,所以BE∥平面PA D.………………8分(2)因为AB
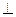 平面PAD,PA,
平面PAD,PA,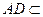 平面PAD,
平面PAD,所以
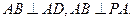 ……………………10分
……………………10分因为
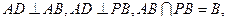
所以
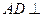 平面PA B.………
平面PA B.……… ………12分
………12分又
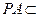 平面PAB,所以
平面PAB,所以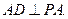
因为
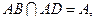 故PA
故PA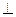 面ABCD.……………………14分
面ABCD.……………………14分
练习册系列答案
相关题目
 中,
中, ,
, 平面
平面 .PA=4,AD=2,AB=
.PA=4,AD=2,AB=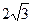 ,BC=6
,BC=6 平面
平面 ;
;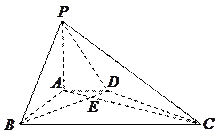
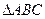 与
与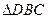 都是边长为
都是边长为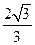 的等边三角形,且平面
的等边三角形,且平面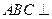 平面
平面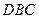 ,过点
,过点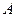 作
作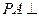 平面
平面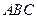 ,且
,且 .
. 与平面
与平面 与底面
与底面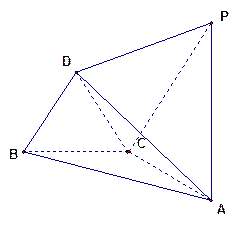
 中,
中,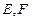 分别是
分别是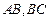 的中点,
的中点,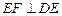 且
且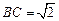 ,若此正三棱锥的四个顶点都在球O的面上,则球O的体积是( )
,若此正三棱锥的四个顶点都在球O的面上,则球O的体积是( )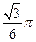
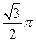
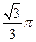
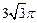
 ,则A—BCD的体积为
,则A—BCD的体积为