题目内容
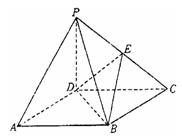
(本小题满分12分)如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB.
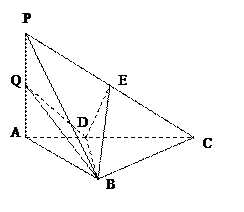
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC//平面BDQ.
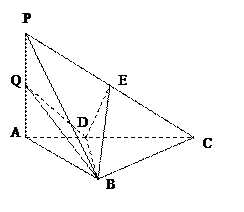
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC//平面BDQ.
(Ⅰ)证明:由等腰三角形PBC,得BE⊥PC
又DE垂直平分PC,∴DE⊥PC ∴PC⊥平面BDE,………… 4分
(Ⅱ)由(Ⅰ),有PC⊥BD
因为 PA⊥底面ABC ,所以PA⊥BD
BD⊥平面PAC,所以点Q是线段PA上任一点都有BD⊥DQ ………………………………… 8分
(Ⅲ)解:不妨令PA=AB=1,有PB=BC=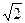 计算得AD=
计算得AD=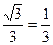 AC 所以点Q在线段PA的
AC 所以点Q在线段PA的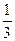 处,即AQ=
处,即AQ=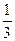 AP时,PC//QD,从而PC//平面BDQ . ……………………………………… 12分
AP时,PC//QD,从而PC//平面BDQ . ……………………………………… 12分
又DE垂直平分PC,∴DE⊥PC ∴PC⊥平面BDE,………… 4分
(Ⅱ)由(Ⅰ),有PC⊥BD
因为 PA⊥底面ABC ,所以PA⊥BD
BD⊥平面PAC,所以点Q是线段PA上任一点都有BD⊥DQ ………………………………… 8分
(Ⅲ)解:不妨令PA=AB=1,有PB=BC=
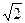 计算得AD=
计算得AD=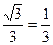 AC 所以点Q在线段PA的
AC 所以点Q在线段PA的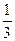 处,即AQ=
处,即AQ=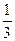 AP时,PC//QD,从而PC//平面BDQ . ……………………………………… 12分
AP时,PC//QD,从而PC//平面BDQ . ……………………………………… 12分
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 ,CD=1
,CD=1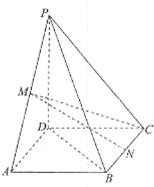
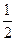 AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点. 0°。
0°。
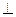 平面PAD,E为PC的中点.
平面PAD,E为PC的中点.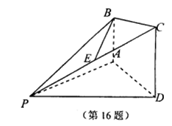
 ,E为SD的中点。
,E为SD的中点。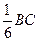 ,求证:EF∥平面SAB;
,求证:EF∥平面SAB; ?
?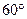 圈上有A、B两点,它们的经度相差
圈上有A、B两点,它们的经度相差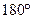 ,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )
,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )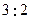 B.
B. 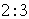 C.
C. 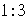 D.
D. 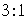
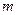 ,
, 和平面
和平面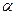 ,
,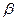 ,
,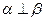 的一个充分条件是( )
的一个充分条件是( )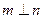 ,
,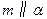 ,
,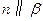
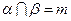 ,
,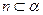
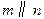 ,
,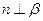 ,
,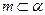
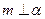 ,
,