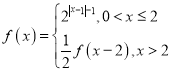题目内容
【题目】已知函数![]() ,且数列
,且数列![]() 满足
满足![]() .
.
(1)若数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(2)若对任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,由已知条件得出
,由已知条件得出![]() ,由
,由![]() 和
和![]() 可得出关于
可得出关于![]() 和
和![]() 的方程组,解出这两个量的值,利用等差数列的通项公式可求得
的方程组,解出这两个量的值,利用等差数列的通项公式可求得![]() ;
;
(2)推导出![]() ,可知数列
,可知数列![]() 中的奇数项和偶数项分别成以
中的奇数项和偶数项分别成以![]() 为公差的等差数列,以此求出数列
为公差的等差数列,以此求出数列![]() 的通项公式,然后分
的通项公式,然后分![]() 为奇数和偶数两种情况讨论,结合
为奇数和偶数两种情况讨论,结合![]() 恒成立,利用参变量分离法可求得
恒成立,利用参变量分离法可求得![]() 的取值范围.
的取值范围.
(1)设等差数列![]() 的公差为
的公差为![]() ,依题意得
,依题意得![]() ,故
,故![]() ,
,
则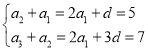 ,解得
,解得![]() ,
,![]()
因此,数列![]() 的通项公式为
的通项公式为![]() ;
;
(2)由(1)知,当![]() 时,
时,![]() ,①,
,①,![]() ,②
,②
两式相减得![]() ,
,
![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列,数列
为公差的等差数列,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列
又![]()
![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ;
;
当![]() 为奇数时,
为奇数时,![]() .
.
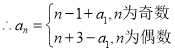 .
.
因为对任意的![]() 都有
都有![]() 成立,
成立,
当![]() 为奇数时,
为奇数时,![]() 恒成立,
恒成立,
![]() 在
在![]() 为奇数时恒成立,
为奇数时恒成立,![]() 即,
即,![]() ;
;
同理当![]() 为偶数时,
为偶数时,![]() 恒成立,
恒成立,
![]() 在
在![]() 为偶数时恒成立,
为偶数时恒成立,![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目