题目内容
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
【答案】每天应生产A型桌子2张,B型桌子3张才能获得最大利润,最大利润为13千元.
【解析】
本试题主要是考查了线性规划问题中的最优解的求解在实际生活中的运用.
根据题意设出变量设每天生产A型桌子x张,B型桌子y张,得到不等式区域,以及目标函数,作图,分析最优解.
解:设每天生产A型桌子x张,B型桌子y张,则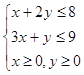 ……2分
……2分
目标函数为:z=2x+3y……4分
作出可行域:
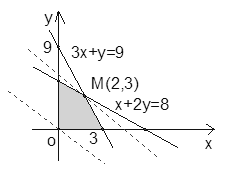 ……6分
……6分
把直线![]() :2x+3y=0向右上方平移至
:2x+3y=0向右上方平移至![]() 的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值……8分
的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值……8分
解方程![]() 得M的坐标为(2,3).
得M的坐标为(2,3).
答:每天应生产A型桌子2张,B型桌子3张才能获得最大利润.……12分

【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了![]() 天.得到的统计数据如下表,
天.得到的统计数据如下表,![]() 为收费标准(单位:元/日),
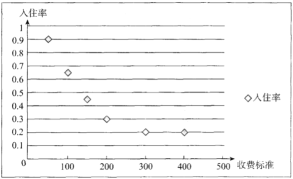
为收费标准(单位:元/日),![]() 为入住天数(单位:),以频率作为各自的“入住率”,收费标准
为入住天数(单位:),以频率作为各自的“入住率”,收费标准![]() 与“入住率”
与“入住率”![]() 的散点图如图
的散点图如图
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若从以上六家“农家乐”中随机抽取两家深入调查,记![]() 为“入住率”超过
为“入住率”超过![]() 的农家乐的个数,求
的农家乐的个数,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散点图判断
,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(
哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(![]() 结果保留一位小数)
结果保留一位小数)
(3)若一年按![]() 天计算,试估计收费标准为多少时,年销售额
天计算,试估计收费标准为多少时,年销售额![]()
![]() 入住率
入住率![]() 收费标准
收费标准![]() )
)
参考数据: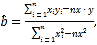
![]()
![]()
![]()
【题目】第十三届全国人大第二次会议于2019年3月5日在北京开幕.为广泛了解民意,某人大代表利用网站进行民意调查.数据调查显示,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组
.现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
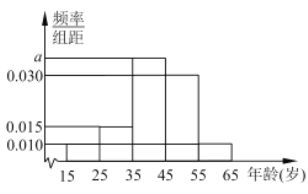
(1)求![]() ;
;
(2)现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人接受现场访谈,求这两人恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的中老年人有10人,问是否有![]() 的把握认为是否关注民生与年龄有关?
的把握认为是否关注民生与年龄有关?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
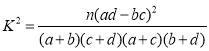 ,
,![]() .
.