题目内容
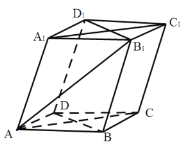
【题目】已知平面四边形![]() 中,
中,![]() ,
,![]() ,再将
,再将![]() 沿着
沿着![]() 翻折成三棱锥
翻折成三棱锥![]() 的过程中,直线
的过程中,直线![]() 与平面
与平面![]() 所成角均小于直线
所成角均小于直线![]() 与平面
与平面![]() 所成角,设二面角
所成角,设二面角![]() ,
,![]() 的大小分别为
的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.存在
C.存在![]() D.存在
D.存在![]()
【答案】A
【解析】
根据条件在![]() 沿着
沿着![]() 翻折成三棱锥
翻折成三棱锥![]() 的过程中,直线
的过程中,直线![]() 与平面
与平面![]() 所成角均小于直线
所成角均小于直线![]() 与平面
与平面![]() 所成角,可得
所成角,可得![]() ,过点
,过点![]() 作
作![]()
![]() 平面
平面![]() ,为
,为![]() 垂足,过
垂足,过![]() 作
作![]()
![]()
![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]()
![]()
![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() 根据
根据![]() ,
,![]() ,可得
,可得![]()
![]()
![]() ,且
,且![]() ,
,![]() ,所以有
,所以有![]() ,从而可得答案.
,从而可得答案.
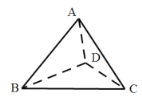
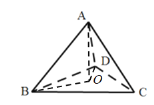
过点![]() 作
作![]()
![]() 平面
平面![]() ,为
,为![]() 垂足,连接
垂足,连接![]() .
.
则![]() 分别为直线
分别为直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角.
所成角.
所以![]() .
.
又![]() 与平面
与平面![]() 所成角均小于直线
所成角均小于直线![]() 与平面
与平面![]() 所成角.
所成角.
所以![]() ,即
,即![]() .
.
平面四边形![]() 中,
中,![]() ,则四点
,则四点![]() 共圆.
共圆.
![]() ,设
,设![]() 的垂直平分线为
的垂直平分线为![]() ,将
,将![]() 沿着
沿着![]() 折起.
折起.
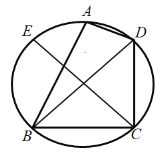
![]() 为该圆的一条直径,由
为该圆的一条直径,由![]() ,所以点
,所以点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在半圆
在半圆![]() 内,如图.
内,如图.
所以点![]() 到直线
到直线![]() 的距离大于到直线
的距离大于到直线![]() 的距离.
的距离.
过![]() 作
作![]()
![]()
![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]()
![]()
![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() ,如图
,如图
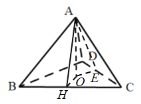
则![]()
![]()
![]() ,
,
由![]() 平面
平面![]() ,所以
,所以![]()
![]()
![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]()
![]() 平面
平面![]() .
.
所以![]()
![]()
![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() .
.
同理可得:![]() .由
.由![]() 在半圆
在半圆![]() 内,则
内,则![]() 为锐角.
为锐角.
![]() ,则
,则![]()
所以![]()
故选:A.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】为了解广大学生家长对校园食品安全的认识,某市食品安全检测部门对该市家长进行了一次校园食品安全网络知识问卷调查,每一位学生家长仅有一次参加机会,现对有效问卷进行整理,并随机抽取出了200份答卷,统计这些答卷的得分(满分:100分)制出的频率分布直方图如图所示,由频率分布直方图可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
近似为这200人得分的平均值(同一组数据用该组区间的中点值作为代表).
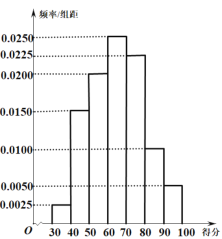
(1)请利用正态分布的知识求![]() ;
;
(2)该市食品安全检测部门为此次参加问卷调查的学生家长制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费:
的可以获赠1次随机话费:
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) |
|
|
概率 |
|
|
市食品安全检测部门预计参加此次活动的家长约5000人,请依据以上数据估计此次活动可能赠送出多少话费?
附:①![]() ;②若
;②若![]() ;则
;则![]() ,
,![]() ,
,![]() .
.
【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.