题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,证明:曲线
,证明:曲线![]() 没有经过坐标原点的切线.
没有经过坐标原点的切线.
【答案】(1)在![]() 单调递减,在
单调递减,在![]() 单调递增;(2)证明见解析
单调递增;(2)证明见解析
【解析】
(1)先求得导函数,根据导函数的符号即可判断单调区间.
(2)先讨论过原点的切线斜率是否存在.当斜率不存在时,切线为y轴,分析可知不成立.当斜率存在时,可设出切线方程和切点坐标.建立方程组,判断方程组无解,即可证明不存在这样的切线.
(1)![]() 定义域为
定义域为![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)因为![]() 定义域为
定义域为![]() ,所以
,所以![]() 轴不是曲线
轴不是曲线![]() 的切线.
的切线.
当经过坐标原点的直线不是![]() 轴时,设
轴时,设![]() 是曲线
是曲线![]() 的切线,切点是
的切线,切点是![]() .
.
因为![]() ,所以
,所以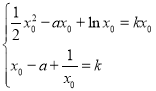 .
.
消去![]() 得
得![]() ,即
,即![]() .
.
由(1)知![]() 在
在![]() 处取得最小值,则
处取得最小值,则![]() ,
,
所以![]() 无解.
无解.
因此曲线![]() 没有经过坐标原点的切线.
没有经过坐标原点的切线.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取![]() 名学生的物理成绩(百分制)作为样本,按成绩分成5组:
名学生的物理成绩(百分制)作为样本,按成绩分成5组:![]() ,频率分布直方图如图所示,成绩落在
,频率分布直方图如图所示,成绩落在![]() 中的人数为20.
中的人数为20.

男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(1)求![]() 和
和![]() 的值;
的值;
(2)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数
和中位数![]() ;
;
(3)成绩在80分以上(含80分)为优秀,样本中成绩落在![]() 中的男、女生人数比为1:2,成绩落在
中的男、女生人数比为1:2,成绩落在![]() 中的男、女生人数比为3:2,完成
中的男、女生人数比为3:2,完成![]() 列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:
| 0.50 | 0.05 | 0.025 | 0.005 |
| 0.455 | 3.841 | 5.024 | 7.879 |