题目内容
【题目】已知函数
．
Ⅰ
当
时，
取得极值，求
的值并判断是极大值点还是极小值点；
Ⅱ当函数有两个极值点
，
，且
时，总有
成立，求
的取值范围．
【答案】（Ⅰ）
，
为极大值点（Ⅱ）
.
【解析】
（Ⅰ）求出函数的导数，求出a的值，得到函数的单调区间，求出函数的极值点即可；
（Ⅱ）求出函数极值点，问题转化为
[2lnx1
]＞0，根据0＜x1＜1时，
0.1＜x1＜2时，
0．即h（x）＝2lnx
（0＜x＜2），通过讨论t的范围求出函数的单调性，从而确定t的范围即可．
（Ⅰ）
，
，则
从而
，所以
时，
，
为增函数；
时，
，为减函数，所以为极大值点.
（Ⅱ）函数的定义域为
，有两个极值点
，
，则
在上有两个不等的正实根，所以
，
由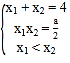
可得
从而问题转化为在
，且
时
成立.
即证
成立.
即证
即证
亦即证 
. ①
令
则
1)当
时，
，则
在
上为增函数且
，①式在
上不成立.
2)当
时，
若
，即
时，
，所以在上为减函数且，
、
在区间
及
上同号，故①式成立.
若
，即
时，
的对称轴
，
令
，则
时，
，不合题意.
综上可知：满足题意.
【题目】田忌赛马是
史记
中记载的一个故事，说的是齐国将军田忌经常与齐国众公子赛马，孙膑发也们的马脚力都差不多，都分为上、中、下三等
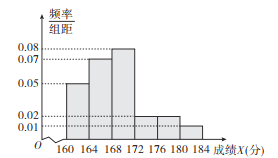
于是孙膑给田忌将军制定了一个必胜策略：比赛即将开始时，他让田忌用下等马对战公子们的上等马，用上等马对战公子们的中等马，用中等马对战公子们的下等马，从而使田忌赢得公子们许多赌注假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示：
田忌的马 | 上等马 | 中等马 | 下等马 |
上等马 |
|
| 1 |
中等马 |
|
|
|
下等马 | 0 |
|
|
比赛规则规定：一次比由三场赛马组成，每场由公子和田忌各出一匹马出骞，结果只有胜和负两种，并且毎一方三场赛马的马的等级各不相同，三场比赛中至少获胜两场的一方为最终胜利者．
如果按孙膑的策略比赛一次，求田忌获胜的概率；
如果比赛约定，只能同等级马对战，每次比赛赌注1000金，即胜利者赢得对方1000金，每月比赛一次，求田忌一年赛马获利的数学期望．
