题目内容
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取![]() 名学生的物理成绩(百分制)作为样本,按成绩分成5组:
名学生的物理成绩(百分制)作为样本,按成绩分成5组:![]() ,频率分布直方图如图所示,成绩落在
,频率分布直方图如图所示,成绩落在![]() 中的人数为20.
中的人数为20.

男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(1)求![]() 和
和![]() 的值;
的值;
(2)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数
和中位数![]() ;
;
(3)成绩在80分以上(含80分)为优秀,样本中成绩落在![]() 中的男、女生人数比为1:2,成绩落在
中的男、女生人数比为1:2,成绩落在![]() 中的男、女生人数比为3:2,完成
中的男、女生人数比为3:2,完成![]() 列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:
| 0.50 | 0.05 | 0.025 | 0.005 |
| 0.455 | 3.841 | 5.024 | 7.879 |
【答案】(1)![]() (2)
(2)![]() ,
,![]() (3)没有95%的把握
(3)没有95%的把握
【解析】
试题分析:(1)根据频率分布直方图中小长方形面积等于对应区域概率得![]() 解得
解得![]() 再根据频率等于频数除以总数得
再根据频率等于频数除以总数得![]() (2)利用组中值求平均数
(2)利用组中值求平均数![]() 由中位数定义知中位数落在
由中位数定义知中位数落在![]() 中,所以
中,所以![]() ,解得
,解得![]() (3)先根据比例关系确定优秀的男生为6人,女生为4人;不优秀的男生为10人,女生为20人.再根据卡方公式计算
(3)先根据比例关系确定优秀的男生为6人,女生为4人;不优秀的男生为10人,女生为20人.再根据卡方公式计算![]() ,比较参考系数得结论
,比较参考系数得结论
试题解析:(1)![]()
(2)由频率分布直方图可知各组的频率分别为0.05,0.2,0.5,0.15,0.1,
所以![]() ,
,
设中位数为![]() ,则
,则![]() ,得
,得![]() .
.
(3)优秀的男生为6人,女生为4人;
不优秀的男生为10人,女生为20人.
所以![]() 列联表如下表:
列联表如下表:
男生 | 女生 | 合计 | |
优秀 | 6 | 4 | 10 |
不优秀 | 10 | 20 | 30 |
合计 | 16 | 24 | 40 |
所以![]() ,
,
所以没有95%的把握认为物理成绩优秀与性别有关

【题目】某中学调查了某班全部45名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加演讲社团 | 2 | 30 |
(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;
(II) 在既参加书法社团又参加演讲社团的8名同学中,有5名男同学![]() ,3名女同学
,3名女同学![]() ,现从这5名男同学和3名女同学中各随机选1人,求
,现从这5名男同学和3名女同学中各随机选1人,求![]() 被选中且
被选中且![]() 未被选中的概率。
未被选中的概率。
【题目】总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
A. 08 B. 02 C. 01 D. 07
【题目】在一次文、理学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩为![]() ,文综成绩为
,文综成绩为![]() ,
,![]() 为
为![]() ,将
,将![]() 值分组统计制成下表:
值分组统计制成下表:
分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) | [120,140] |
频数 | 4 | 18 | 42 | 66 | 48 | 20 | 2 |
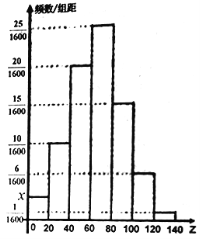
并将其中女生的![]() 值分布情况制成频率分布直方图(如图所示).
值分布情况制成频率分布直方图(如图所示).
(1)若已知直方图中[60,80)频数为25,试分别估计全体学生中,![]() 的男、女生人数;
的男、女生人数;
(2)记![]() 的平均数为
的平均数为![]() ,如果
,如果![]() 称为整体具有学科学习倾向,试估计高一年段女生的
称为整体具有学科学习倾向,试估计高一年段女生的![]() 值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.
值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.