题目内容
已知函数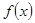 对任意
对任意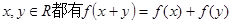 ,且x>0时
,且x>0时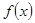 <0,
<0,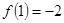 。①求
。①求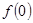
②求证: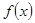 为奇函数;
为奇函数;
③ 求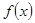 在
在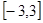 上的最大值和最小值。
上的最大值和最小值。
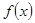 对任意
对任意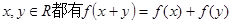 ,且x>0时
,且x>0时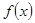 <0,
<0,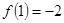 。①求
。①求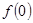
②求证:
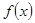 为奇函数;
为奇函数;③ 求
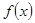 在
在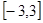 上的最大值和最小值。
上的最大值和最小值。①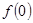 =0 ②证明:见解析 ③.函数在
=0 ②证明:见解析 ③.函数在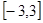 上的最大值为6,最小值为-6。
上的最大值为6,最小值为-6。
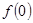 =0 ②证明:见解析 ③.函数在
=0 ②证明:见解析 ③.函数在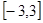 上的最大值为6,最小值为-6。
上的最大值为6,最小值为-6。(1)赋具体数值与赋式子相结合,利用函数奇偶性的定义证明奇偶性;(2)先利用赋值思想证明函数在给定区间上的单调性,在利用赋值法求出函数的最值
①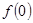 =0
=0
②证明:因为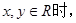
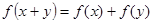 所以令y=-x,
所以令y=-x,
则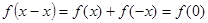
所以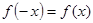
所以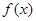 为奇函数。
为奇函数。
③.设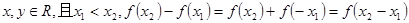
因为x>0时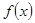 <0,所以
<0,所以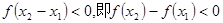 ,
,
所以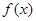 为减函数。所以
为减函数。所以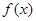 在
在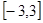 上的最大值为
上的最大值为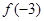 ,最小值为
,最小值为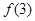 。因为
。因为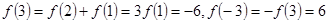 ,所以函数在
,所以函数在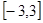 上的最大值为6,最小值为-6。
上的最大值为6,最小值为-6。
①
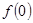 =0
=0②证明:因为
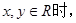
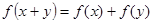 所以令y=-x,
所以令y=-x,则
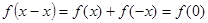
所以
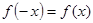
所以
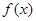 为奇函数。
为奇函数。③.设
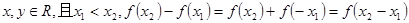
因为x>0时
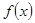 <0,所以
<0,所以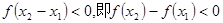 ,
,所以
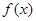 为减函数。所以
为减函数。所以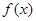 在
在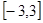 上的最大值为
上的最大值为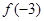 ,最小值为
,最小值为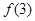 。因为
。因为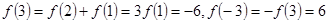 ,所以函数在
,所以函数在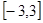 上的最大值为6,最小值为-6。
上的最大值为6,最小值为-6。
练习册系列答案
相关题目
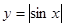 的一个单调增区间是( )
的一个单调增区间是( )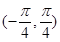
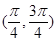
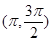
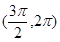
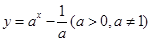 的图象可能是( )
的图象可能是( )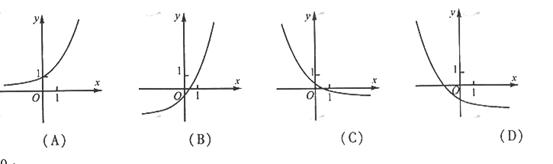
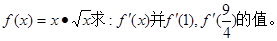
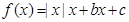 ,则下列命题中正确命题的序号有__________.
,则下列命题中正确命题的序号有__________.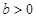 时,函数
时,函数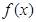 在R上是单调增函数;
在R上是单调增函数;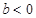 时,函数
时,函数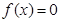 可能有三个实数根.
可能有三个实数根.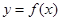 满足
满足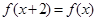 ,且当
,且当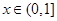 时单调递增,则( )
时单调递增,则( )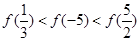
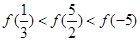
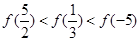
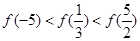
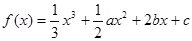 ,若当
,若当 时,
时,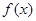 取得极大值,
取得极大值,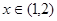 时,
时,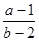 的取值范围是 .
的取值范围是 .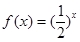 ,且
,且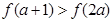 ,则实数
,则实数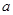 的取值范围是 。
的取值范围是 。