Question

【题目】某市规定，高中学生三年在校期间参加不少于小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段，，，

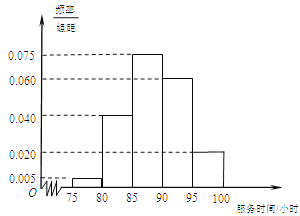
，（单位：小时）进行统计，其频率分布直方图如图所示．

（Ⅰ）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计

从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；

（Ⅱ）从全市高中学生（人数很多）中任意选取3位学生，记为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量的分布列和数学期望．

Answer 1

【答案】（Ⅰ）（Ⅱ）

	0	1	2	3

【解析】

试题分析：（Ⅰ）根据频率分布直方图中小长方形面积为频率，而频数为总数与频率之积. 因此参加社区服务时间在时间段小时的学生人数为（人），参加社区服务时间在时间段小时的学生人数为（人）．所以抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为人．概率估计为（Ⅱ）随机变量的可能取值为．由（Ⅰ）可知，概率为因为 ~，所以．随机变量的分布列为

	0	1	2	3

解：（Ⅰ）根据题意，

参加社区服务时间在时间段小时的学生人数为（人），

参加社区服务时间在时间段小时的学生人数为（人）．

所以抽取的200位学生中，参加社区服务时间不少于90小时的学生人数为人．

所以从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的

概率估计为 5分

（Ⅱ）由（Ⅰ）可知，从全市高中生中任意选取1人，其参加社区服务时间不少于90小时的概率为

由已知得，随机变量的可能取值为．

所以；

；

；

．

随机变量的分布列为

	0	1	2	3

因为 ~，所以． 13分