Question

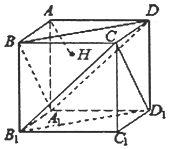
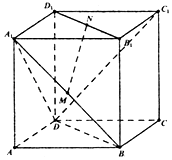
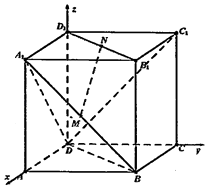
【题目】如图，在正方体ABCD﹣A1B1C1D1中，点M、N分别是面对角线A1B与B1D1的中点，设 = ， = ， = ．

（1）以{ ， ， }为基底，表示向量 ；
（2）求证：MN∥平面BCC1B1；
（3）求直线MN与平面A1BD所成角的正弦值．

Answer 1

【答案】
（1）解：
（2）证明：连A1C1、BC1，则N为A1C1的中点，

又M为A1B的中点，

∴MN∥BC1，

又MN平面BCC1B1，BC1平面BCC1B1，

∴MN∥平面BCC1B1

（3）解：∵DA、DC、DD1两两垂直，

∴可以D为原点，DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系D﹣xyz．

设正方体棱长为2，

则M（2，1，1），N（1，1，2），A1（2，0，2），B（2，2，0），

D（0，0，0），A（2，0，0），C1（0，2，2），

∴ ， ， ， ，

∵ ， ，

∴ ， ，

∴ 为平面A1BD的法向量，

设直线MN与平面A1BD所成的角为θ，

则 ，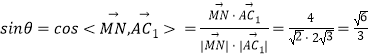

所以直线MN与平面A1BD所成角的正弦值为 ．

【解析】（1）利用向量的加法，即可得出结论；（2）连A1C1、BC1 ， 则N为A1C1的中点，证明MN∥BC1 ， 即可证明结论；（3）以D为原点，DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系D﹣xyz，求出平面A1BD的法向量，即可求直线MN与平面A1BD所成角的正弦值．
【考点精析】关于本题考查的直线与平面平行的判定和空间角的异面直线所成的角，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则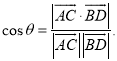才能得出正确答案．