题目内容
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,动点
,动点![]() 在椭圆上,且使得
在椭圆上,且使得![]() 的点
的点![]() 恰有两个,动点
恰有两个,动点![]() 到焦点
到焦点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,以椭圆![]() 的长轴为直径作圆
的长轴为直径作圆![]() ,过直线
,过直线![]() 上的动点
上的动点![]() 作圆
作圆![]() 的两条切线,设切点分别为
的两条切线,设切点分别为![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.

【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由对称知识有![]() ,
, ![]() ,又
,又![]() ,求出
,求出![]() ,再写出椭圆方程;(2)写出圆
,再写出椭圆方程;(2)写出圆![]() 的方程,设出
的方程,设出![]() 点的坐标,写出直线AB的方程,求出原点
点的坐标,写出直线AB的方程,求出原点![]() 到直线
到直线![]() 的距离表达式,联立直线AB方程和椭圆方程,求出
的距离表达式,联立直线AB方程和椭圆方程,求出![]() 的表达式,利用单调性求出范围。
的表达式,利用单调性求出范围。
试题解析;(1)![]()
(2)圆![]() 的方程为
的方程为![]() ,设直线
,设直线![]() 上动点
上动点![]() 的坐标为
的坐标为![]() ,设
,设![]() ,
, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,又
,又![]() 在直线
在直线![]() 和
和![]() 上,即
上,即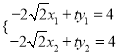 ,故直线
,故直线![]() 的方程为
的方程为![]() .
.
由原点![]() 到直线
到直线![]() 的距离
的距离![]() 得
得![]() ,
,
联立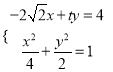 ,消去
,消去![]() 得
得![]() ,设
,设![]() ,
, ![]() ,
,
则![]() ,从而
,从而![]() ,
,
则![]() ,又设
,又设![]() ,
,
所以![]() ,设
,设![]() ,
,
所以由![]() 得
得![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
即![]() .
.

练习册系列答案
相关题目
【题目】以下是某地搜集到的新房屋的销售价格![]() 和房屋的面积
和房屋的面积![]() 的数据:
的数据:
房屋面积( | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150![]() 时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]()